
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点,延长BC至点F,使CF=CE.
(1)∠ABC的度数.
(2)求证:BE=FE.
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得![]() 的值最大的点,Q是y轴上使得QA十QB的值最小的点,则
的值最大的点,Q是y轴上使得QA十QB的值最小的点,则![]() = ▲ .
= ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,折叠长方形(四个角都是直角)的一边AD使点D落在BC边的点F处,已知AB=DC=8cm,AD=BC=10cm,

求:(1)求BF长度;
(2)求CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用配方法求出抛物线![]() 的顶点坐标、对称轴、最大值或最小值;若将抛物线
的顶点坐标、对称轴、最大值或最小值;若将抛物线![]() 先向左平移
先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得抛物线的函数关系式为________.
个单位,所得抛物线的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线一点,点O是线段AD上一点,OP=OC.
(1)已知∠APO=18°,求∠DCO的度数;
(2)求证:△OPC是等边三角形;
(3)求证:AC=AO+AP.

查看答案和解析>>
科目:初中数学 来源: 题型:
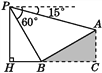
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
A. 15米 B. 20![]() 米 C. 20
米 C. 20![]() 米 D. 10
米 D. 10![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
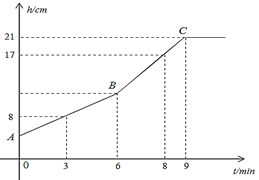
【题目】某兴趣小组观察下雨天学校池塘水面高度h(单位:cm)与观察时间t(单位:min)的关系,并根据当天观察数据画出了如图所示的图象,请你结合图象回答下列问题:
(1)求线段BC的表达式;
(2)试求出池塘原有水面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足分别为E、F,如图①。
(1)请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?并说明理由。
(2)若点P在DC的延长线上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?直接写出结论。
(3)若点P在CD的延长线上呢,如图③,直接写出结论。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com