
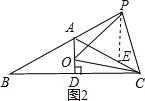
【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线一点,点O是线段AD上一点,OP=OC.
(1)已知∠APO=18°,求∠DCO的度数;
(2)求证:△OPC是等边三角形;
(3)求证:AC=AO+AP.

【答案】(1)12°;(2)见解析;(3)见解析
【解析】
(1)利用等边对等角,即可证得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;
(2)证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;
(3)首先证明△OPA≌△CPE,则AO=CE,AC=AE+CE=AO+AP.
(1)解:如图1,连接OB,
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°-∠BAD=30°
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
∴∠DCO=30°-∠APO=30°-18°=12°;
(2)证明:∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
(3)证明:如图2,在AC上截取AE=PA
 ,
,
∵∠PAE=180°-∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
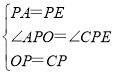 ,
,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于点P,交AC于点M,连接PC.
(Ⅰ)若∠A=60°,∠ACP=24°,求∠ABP的度数;
(Ⅱ)若AB=BC,BM2+CM2=m2(m>0),△PCM的周长为m+2时,求△BCM的面积(用含m的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂里有许多剩余的三角形边角料,找出一块△ABC,测得∠C=90°(如图),现要从这块三角形上剪出一个半圆O,做成玩具,要求:使半圆O与三角形的两边AB、AC相切,切点分别为D、C,且与BC交于点E.
(1)在图中设计出符合要求的方案示意图.(要求:尺规作图,不写作法,保留作图痕迹).
(2)Rt△ABC中,AC=3,AB=5,连接AO,求出AO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点F,BH⊥AB于点B,点M是BC的中点,连接FM并延长交BH于点H.

(1)如图①所示,若∠ABC=30°,求证:DF+BH=![]() BD;
BD;
(2)如图②所示,若∠ABC=45°,如图③所示,若∠ABC=60°(点M与点D重合),猜想线段DF、BH与BD之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点,延长BC至点F,使CF=CE.
(1)∠ABC的度数.
(2)求证:BE=FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是
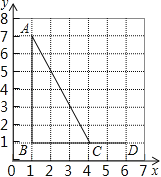
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5。一只蚂蚁如果要沿着长方体的表面从点A爬到点B,爬行的最短路程是( )
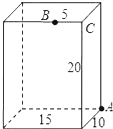
A.25B.![]() C.35D.无法确定
C.35D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,联结EF.
(1)如图,当点D在线段CB上时,
①求证:△AEF≌△ADC;
②联结BE,设线段CD=x,线段BE=y,求y关于x的函数解析式及定义域;
(2)当∠DAB=15°时,求△ADE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com