
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,联结EF.
(1)如图,当点D在线段CB上时,
①求证:△AEF≌△ADC;
②联结BE,设线段CD=x,线段BE=y,求y关于x的函数解析式及定义域;
(2)当∠DAB=15°时,求△ADE的面积.

【答案】(1)①证明见解析;②函数的解析式是y=![]() ,定义域是0<x≤5
,定义域是0<x≤5![]() ;(2)△ADE的面积为
;(2)△ADE的面积为![]() 或50
或50![]() +75.
+75.
【解析】
(1)①在直角三角形![]() 中,由30度所对的直角边等于斜边的一半求出
中,由30度所对的直角边等于斜边的一半求出![]() 的长,再由
的长,再由![]() 为
为![]() 中点,得到
中点,得到![]() ,确定出三角形
,确定出三角形![]() 为等边三角形,利用等式的性质得到一对角相等,再由
为等边三角形,利用等式的性质得到一对角相等,再由![]() ,利用
,利用![]() 即可得证;
即可得证;
②由全等三角形对应角相等得到![]() 为直角,
为直角,![]() ,在三角形
,在三角形![]() 中,利用勾股定理即可列出
中,利用勾股定理即可列出![]() 关于
关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
(2)分两种情况考虑:①当点D在线段![]() 上时;②当点D在线段
上时;②当点D在线段![]() 的延长线上时,分别求出三角形
的延长线上时,分别求出三角形![]() 面积即可.
面积即可.
(1)①在Rt△ABC中,
∵∠B=30°,AB=10,
∴∠CAB=60°,AC=![]() AB=5,
AB=5,
∵点F是AB的中点,
∴AF=![]() AB=5,
AB=5,
∴AC=AF,
∵△ADE是等边三角形,
∴AD=AE,∠EAD=60°,
∵∠CAB=∠EAD,即∠CAD+∠DAB=∠FAE+∠DAB,
∴∠CAD=∠FAE,
在△AEF和△ADC中,
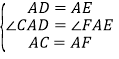 ,
,
∴△AEF≌△ADC(SAS);
②∵△AEF≌△ADC,
∴∠AFE=∠C=90°,EF=CD=x,
又∵点F是AB的中点,
∴AE=BE=y,
在Rt△AEF中,勾股定理可得:y2=25+x2,
∴函数的解析式是![]() ,定义域是
,定义域是![]() ;
;
(2)①当点D在线段CB上时,
由∠DAB=15°,可得∠CAD=45°,△ADC是等腰直角三角形,
∴AD2=50,
△ADE的面积为![]() ;
;
②当点D在线段CB的延长线上时,
由∠DAB=15°,可得∠ADB=15°,BD=BA=10,
∴在Rt△ACD中,勾股定理可得![]() ,
,
△ADE的面积为![]() ,
,
综上所述,△ADE的面积为![]() 或
或![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线一点,点O是线段AD上一点,OP=OC.
(1)已知∠APO=18°,求∠DCO的度数;
(2)求证:△OPC是等边三角形;
(3)求证:AC=AO+AP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x +m和y=-
x +m和y=-![]() x +n的图象都是经过点A(-2,0),且与y轴分别交于B、C两点.
x +n的图象都是经过点A(-2,0),且与y轴分别交于B、C两点.
(1)直接写出B、C两点的坐标B: ;C:
(2)求ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足分别为E、F,如图①。
(1)请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?并说明理由。
(2)若点P在DC的延长线上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?直接写出结论。
(3)若点P在CD的延长线上呢,如图③,直接写出结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,D是边长为4㎝的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.


图1 图2
①请说明△PQR是等边三角形的理由;
②若BD=1.3㎝,则AE=_______㎝(填空)
③如图2,当点E恰好与点D重合时,求出BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊿ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向⊿ABC作等腰Rt⊿ABE和等腰Rt⊿ACF,过点E、F作射线GA的垂线,垂足分别为P、Q。
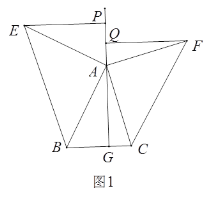
(1)求证:⊿AEP≌⊿BAG;
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
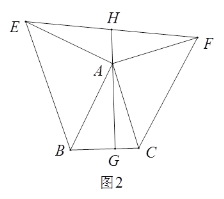
(3)如图2,若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由;
(4)在(3)的条件下,若BC=AG=10,请直接写出S⊿AEF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
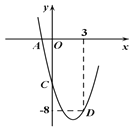
【题目】二次函数![]() 的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).(1)求此二次函数的解析式; (2)用配方法将将此二次函数的解析式写成
的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).(1)求此二次函数的解析式; (2)用配方法将将此二次函数的解析式写成![]() 的形式,并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
的形式,并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com