
【题目】如图,在△ABC中,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于点P,交AC于点M,连接PC.
(Ⅰ)若∠A=60°,∠ACP=24°,求∠ABP的度数;
(Ⅱ)若AB=BC,BM2+CM2=m2(m>0),△PCM的周长为m+2时,求△BCM的面积(用含m的代数式表示).

【答案】(Ⅰ)32°;(Ⅱ)m+1.
【解析】
(Ⅰ)根据线段垂直平分线的性质,可得∠PBC=∠PCB,根据角平分线的定义,可得∠PBC=∠PCB=∠ABP,最后根据三角形内角和定理,即可得到∠ABP的度数;
(Ⅱ)根据直角三角形的性质得到BM⊥AC,求得∠BMC=90°,根据线段垂直平分线的性质得到PB=PC,求得BM+CM=m+2,推出BMCM=2m+2,于是得到结论.
解:(Ⅰ)∵点D是BC边的中点,DE⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠PBC=∠PCB=∠ABP,
∵∠A=60°,∠ACP=24°,
∴∠PBC+∠PCB+∠ABP=120°﹣24°,
∴3∠ABP=120°﹣24°,
∴∠ABP=32°;
(Ⅱ)∵AB=BC,BP平分∠ABC,
∴BM⊥AC,
∴∠BMC=90°,
∵PD⊥BC,点D是BC边的中点,
∴PD垂直平分BC,
∴PB=PC,
∵△PCM的周长为m+2,
∴PM+PC+CM=PM+PB+CM=BM+CM=m+2,
∴(BM+CM)2=BM2+CM2+2BMCM=m2+2BMCM=(m+2)2,
∴BMCM=2m+2,
∴△BCM的面积=![]() BMCM=m+1.
BMCM=m+1.


科目:初中数学 来源: 题型:
【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
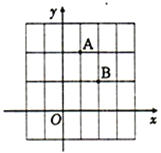
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是![]() 轴上使得∣PA—PB∣的值最大的点,Q是
轴上使得∣PA—PB∣的值最大的点,Q是![]() 轴上使得QA+QB的值最小的点,则OP·OQ=__________.
轴上使得QA+QB的值最小的点,则OP·OQ=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作与探究:如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G点在边BC上,BG=10.
①第一次折叠:当折痕的另一端点F在AB边上时,如图1,求折痕GF的长;
②第二次折叠:当折痕的另一端点F在AD边上时,如图2,证明四边形BGEF为菱形,并求出折痕GF的长.

(2)拓展延伸:通过操作探究发现在矩形纸片ABCD中,AB=5,AD=13.如图3所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A′在BC边上可移动的最大距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线一点,点O是线段AD上一点,OP=OC.
(1)已知∠APO=18°,求∠DCO的度数;
(2)求证:△OPC是等边三角形;
(3)求证:AC=AO+AP.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com