
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

【答案】(1) 45°;(2) P(2,-3);(3)![]() .
.
【解析】
(1)由抛物线解析式可得三角形各点坐标,判断三角形形状,即可得到其内角;
(2)过点D作DH⊥x轴于点H,由不规则图象面积分割求和的方法求得面积,得到点E坐标,再求得直线ED解析式,联立抛物线方程即可得到点P坐标;
(3)先分别表示出点F和点P坐标,再利用已知条件用其坐标表示线段PF的长度,再根据二次函数性质求得其最大值即可.
解:(1)A(-1,0),B(3,0),C(0,-3),D(1,-4).∵OC=OB=3,∴△OBC为等腰直角三角形,∴∠OBC=45°.
(2)过点D作DH⊥x轴于点H,此时S四边形OCDB=S梯形OCDH+S△HBD,∵OH=1,OC=3,HD=4,HB=2,∴S梯形OCDH=·(OC+HD)·OH=,S△HBD=·HD·HB=4,∴S四边形OCDB=![]() .∴S△OCE=S四边形OCDB=
.∴S△OCE=S四边形OCDB=![]() =·OC·OE,∴OE=5,∴E(5,0).∴lDE:y=x-5.∵DE交抛物线于P,设P(x,y),∴x2-2x-3=x-5,解得 x=2 或x=1(D点,舍去),∴xP=2,代入lDE:y=x-5,∴P(2,-3).
=·OC·OE,∴OE=5,∴E(5,0).∴lDE:y=x-5.∵DE交抛物线于P,设P(x,y),∴x2-2x-3=x-5,解得 x=2 或x=1(D点,舍去),∴xP=2,代入lDE:y=x-5,∴P(2,-3).
(3)如图,lBC:y=x-3.∵F在BC上,∴yF=xF-3.∵P在抛物线上,∴yP=x-2xP-3,∴PF=yF-yP=xF-3-(x-2xP-3).∵xP=xF,∴PF=-x+3xP=-(xP-)2+ (1<xP<3),∴当xP=时,线段PF长度最大,最大值为.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=130°,AB、AC的垂直平分线分别交BC于点M、N,则∠MAN等于( )

A.60°B.70°C.80°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
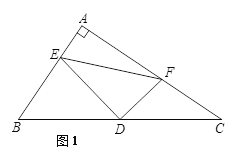

(1)如图1,试说明![]() ;
;
(2)如图2,若AB=AC,BE=12,CF=5,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片OABC放在直角坐标系中,O为原点,C在x的正半轴上,OA=6,OC=10.

(1)写出B的坐标;
(2)在OA上取点E,将△EOC沿EC折叠,使O落在AB边上的D点,求E点坐标;
(3)求直线DE的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com