
【题目】如图,一次函数![]() 与坐标轴交于A、B两点,BC是∠ABO的角平分线.
与坐标轴交于A、B两点,BC是∠ABO的角平分线.
(1)求点A、B的坐标;
(2)求BC所在直线的表达式.

【答案】(1)(0,6),(8,0);(2)y=![]() x+3
x+3
【解析】
(1)分别令x=0与y=0即可求出点A、B的坐标;
(2)根据(1)得出OA与OB的长,然后利用角平分线的性质求出点C的坐标即可得到直线BC的解析式.
解:(1)令y=0,则![]() ,解得:x=8,
,解得:x=8,
∴B的坐标是(8,0),
令x=0,则y=6,
∴A的坐标是(0,6);
(2)如图,过点C作CD⊥AB,垂足为D,

由(1)知OA=6,OB=8,由勾股定理可得:
![]()
∴BC是∠ABO的角平分线,且CD⊥AB
∴CD=OD,设OC=y,
则S△OAB=![]() OAOB=
OAOB=![]() OBy+
OBy+![]() ABy,
ABy,
则6×8=6x+10x,
解得:y=3,
则C的坐标是(0,3)
设直线BC的解析式为y=k1x+b1(k≠0)
∵点(8,0)与(0,3)在直线BC上
∴![]()
解得:
∴直线BC的解析式为y=![]() x+3.
x+3.
故答案为:(1)(0,6),(8,0);(2)y=![]() x+3.
x+3.


科目:初中数学 来源: 题型:
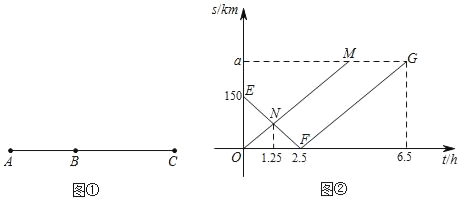
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,一次函数的图象与抛物线交于
三点,一次函数的图象与抛物线交于![]() ,
,![]() 两点.
两点.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 当两函数的函数值都随着
当两函数的函数值都随着![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
![]() 当自变量
当自变量![]() 满足什么范围时,一次函数值大于二次函数值.
满足什么范围时,一次函数值大于二次函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列各题:
(1)先化简,再求代数式(![]() 的值,其中x=
的值,其中x=![]() cos30°+
cos30°+![]() ;
;
(2)已知α是锐角,且sin(α+15°)=![]() .计算
.计算![]() -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+(![]() )-1的值.
)-1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A(0,3),B(4,0),C(﹣1,﹣1),点 P 线段 AB上一动点,将线段 AB 绕原点 O 旋转一周,点 P 的对应点为 P′,则 P′C 的最大值为_____,最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
则下列判断中正确的是( )
A. 拋物线开口向上 B. 拋物线与![]() 轴交于负半轴
轴交于负半轴
C. 当![]() 时,
时,![]() D. 方程
D. 方程![]() 的正根在3与4之间
的正根在3与4之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com