
分析 先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{x}{(x+1)(x-1)}$÷[$\frac{x+2}{2(x-1)}$-$\frac{2}{2(x-1)}$]
=$\frac{x}{(x+1)(x-1)}$÷$\frac{x}{2(x-1)}$
=$\frac{x}{(x+1)(x-1)}$•$\frac{2(x-1)}{x}$
=$\frac{2}{x+1}$,
当x=$\sqrt{2}$-1时,原式=$\frac{2}{\sqrt{2}-1+1}$=$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
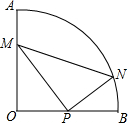 已知:∠AOB=90°,OA=OB=4,P、M、N分别是OB、OA、$\widehat{AB}$上的动点,且∠MPN=90°,PM:PN=3:2,求△PMN周长的最小值.
已知:∠AOB=90°,OA=OB=4,P、M、N分别是OB、OA、$\widehat{AB}$上的动点,且∠MPN=90°,PM:PN=3:2,求△PMN周长的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
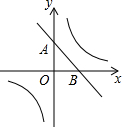 已知直线y=-x+b与双曲线y=$\frac{k}{x}$(k>0).
已知直线y=-x+b与双曲线y=$\frac{k}{x}$(k>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
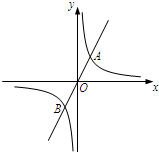 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
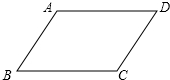 如图,已知?ABCD.
如图,已知?ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com