
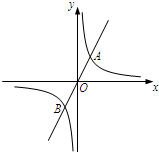
 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,分析 (1)过点A作AD⊥x轴,垂足为D,由点A、B的对称性可知OA=$\sqrt{5}$,根据点在直线上,设点A的坐标为(a,2a),在Rt△OAD中,通过勾股定理即可求出点A的坐标,由点A的坐标利用待定系数法即可求出结论;
(2)由点A、B的对称性结合点A的坐标求出点B的坐标,根据点C在反比例函数图象上,设出点C的坐标为(n,$\frac{2}{n}$),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
解答 解:(1)过点A作AD⊥x轴,垂足为D,如图1所示.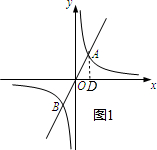
由题意可知点A与点B关于点O中心对称,且AB=2$\sqrt{5}$,
∴OA=OB=$\sqrt{5}$.
设点A的坐标为(a,2a),
在Rt△OAD中,∠ADO=90°,由勾股定理得:
a2+(2a)2=($\sqrt{5}$)2,
解得:a=1,
∴点A的坐标为(1,2).
把A(1,2)代入y=$\frac{k}{x}$中得:2=$\frac{k}{1}$,
解得:k=2.
(2)∵点A的坐标为(1,2),点A、B关于原点O中心对称,
∴点B的坐标为(-1,-2).
设点C的坐标为(n,$\frac{2}{n}$),
△ABC为直角三角形分三种情况:
①∠ABC=90°,则有AB⊥BC,
$\frac{-2-2}{-1-1}$•$\frac{-2-\frac{2}{n}}{-1-n}$=-1,即n2+5n+4,
解得:n1=-4,n2=-1(舍去),
此时点C的坐标为(-4,-$\frac{1}{2}$);
②∠BAC=90°,则有BA⊥AC,
$\frac{-2-2}{-1-1}$•$\frac{\frac{2}{n}-2}{n-1}$=-1,即n2-5n+4=0,
解得:n3=4,n4=1(舍去),
此时点C的坐标为(4,$\frac{1}{2}$);
③∠ACB=90°,则有AC⊥BC,
$\frac{-2-\frac{2}{n}}{-1-n}$•$\frac{2-\frac{2}{n}}{1-n}$=-1,即n2=4,
解得:n5=-2,n6=2,
此时点C的坐标为(-2,-1)或(2,1).
综上所述:当△ABC为直角三角形,点C的坐标为(-4,-$\frac{1}{2}$)、(4,$\frac{1}{2}$)、(-2,-1)或(2,1).
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及垂直的性质,解题的关键是:(1)求出点A的坐标;(2)分情况讨论.本题属于中档题,难度不大,解决该题型题目时,巧妙的利用两直线垂直(斜率存在)斜率之积为-1来解决问题.


科目:初中数学 来源: 题型:解答题
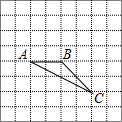 如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
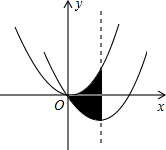 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
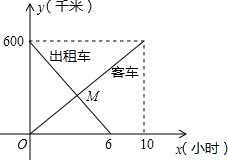 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示.
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
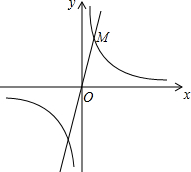 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{4}{x}$的图象与正比例函数y=kx的图象的一个交点为M(1,b).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{4}{x}$的图象与正比例函数y=kx的图象的一个交点为M(1,b).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com