
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.

【考点】正方形的性质;全等三角形的判定与性质.
【专题】几何图形问题.
【分析】(1)由四边形ABCD为正方形,得到AB=AD,∠B=∠D=90°,DC=CB,由E、F分别为DC、BC中点,得出DE=BF,进而证明出两三角形全等;
(2)首先求出DE和CE的长度,再根据S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF得出结果.
【解答】(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠D=∠B=90°,DC=CB,
∵E、F为DC、BC中点,
∴DE=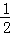 DC,BF=
DC,BF=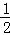 BC,
BC,
∴DE=BF,
在△ADE和△ABF中,
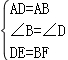 ,
,
∴△ADE≌△ABF(SAS);
(2)解:由题知△ABF、△ADE、△CEF均为直角三角形,
且AB=AD=4,DE=BF=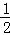 ×4=2,CE=CF=
×4=2,CE=CF=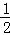 ×4=2,
×4=2,
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF
=4×4﹣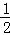 ×4×2﹣
×4×2﹣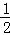 ×4×2﹣
×4×2﹣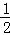 ×2×2
×2×2
=6.
【点评】本题主要考查正方形的性质和全等三角形的证明,解答本题的关键是熟练掌握正方形的性质以及全等三角形的判定定理,此题难度不大.


科目:初中数学 来源: 题型:
已知:a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
解:∵a2c2﹣b2c2=a4﹣b4,①
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2).②
∴c2=a2+b2.③
∴△ABC是直角三角形.
问:
(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号:__________;
(2)错误的原因为__________;
(3)本题正确的解题过程:
查看答案和解析>>
科目:初中数学 来源: 题型:
“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x千克,付款金额为y元,则y与x的函数关系的图象大致是( )
A. B.
B.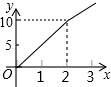 C.
C.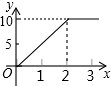 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC是等边三角形.P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( )
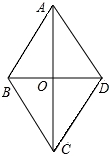
A.7对 B.8对 C.9对 D.10对
查看答案和解析>>
科目:初中数学 来源: 题型:
在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角,从A到B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D的飞行方向角为145°,试求AB与AC之间的夹角为多少度?AD与AC之间的夹角为多少度?并画出从A飞出且方向角为105°的飞行线。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com