
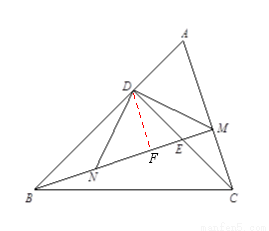
如图,△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,BM交CD于点E,且点E为CD的中点,连接MD,过点D作ND⊥MD于点D,DN交BM于点N.
(1)若BC= ,求△BDE的周长;
,求△BDE的周长;
(2)求证:NE-ME=CM.

(1)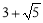 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据等腰三角形的判定和性质求出BD=DC的长,由点E为CD的中点得到DE的长,从而由勾股定理求出BE的长,即可得△BDE的周长.
(2)过点D作DF⊥BM于点F,根据△DEF≌△CEM(AAS)和△BDN≌△CDM(ASA)证得∠DNM=∠DMN=45°和∠DNF=∠NDF=45°,得到DF=NF即可得出结论.
(1)∵∠ABC=45°,CD⊥AB,
∴在Rt△BCD中,∠DBC=∠DCB=45°.
∵BC=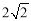 ,∴BD=CD=2.
,∴BD=CD=2.
∵点E为CD中点,∴DE=CE=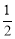 CD=1.
CD=1.
∴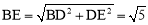 .
.
∴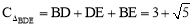 .
.
∴△BDE的周长为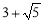 .
.
(2)如图,过点D作DF⊥BM于点F,
∵BM⊥AC,∴∠DFE=∠CME=90°.
在△DEF和△CEM中,∵ ,∴△DEF≌△CEM(AAS).
,∴△DEF≌△CEM(AAS).
∴DF=CM,FE=ME.
∵ND⊥MD,CD⊥AB,∴∠BDN+∠NDE=∠CDM+∠NDE=90°. ∴∠BDN=∠CDM.
∵CD⊥AB,BM⊥AC,∴∠BDE=∠CDA=90°,∠DBE+∠DEB=∠ACD+∠CEM=90°.
∵∠DEB=∠CEM,∴∠DBE=∠ACD.
在△BDN和△CDM中,∵ ,∴△BDN≌△CDM(ASA).
,∴△BDN≌△CDM(ASA).
∴DN=DM.
∴在Rt△DMN中,∠DNM=∠DMN=45°;在Rt△DFN中,∠DNF=∠NDF=45°.
∴DF=NF.
又∵DF=CM,FE=ME,∴NE=NF+FE=CM+ME.
∴NE-ME=CM..
考点:1. 等腰三角形的判定和性质;2.勾股定理;3.全等三角形的判定和性质.


科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:填空题
一个圆锥的侧面展开图是圆心角为120°、半径为15cm的扇形,则圆锥的底面半径为 cm.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷(解析版) 题型:选择题
下列各数中,比-1小的是( )。
A.-2 B.0 C.2 D.3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:选择题
下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第(20)个图形中圆的个数为( )
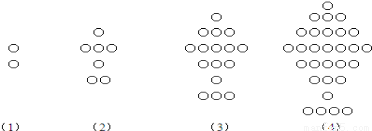
A、781 B、784 C、787 D、678
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:选择题
已知点A、B分别在反比例函数 (x>0),
(x>0), (x>0)的图象上,且OA⊥OB,则
(x>0)的图象上,且OA⊥OB,则 的值为( )
的值为( )

A. B.2 C.
B.2 C. D.3
D.3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省盘锦市中考第一次模拟考试数学试卷(解析版) 题型:解答题
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
点(﹣1,y1),(2,y2),(3,y3)均在函数y= 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y2<y3<y1
C.y1<y2<y3 D.y1<y3<y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com