
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .

【答案】(1)60°;(2)不变化,∠APB=2∠ADB,证明详见解析;(3)30°.
【解析】试题分析:(1)已知AM∥BN,根据两直线平行,同旁内角互补可得∠A+∠ABN=180°,从而求得ABN=120°;已知BC、BD分别平分∠ABP和∠PBN,根据角平分线的定义可得∠CBP=![]() ∠ABP,∠DBP=
∠ABP,∠DBP=![]() ∠NBP,所以∠CBD=
∠NBP,所以∠CBD=![]() ∠ABN=60°;(2)不变化,∠APB=2∠ADB,已知AM∥BN,根据两直线平行,内错角相等即可得∠APB=∠PBN,∠ADB=∠DBN;由BD平分∠PBN,根据角平分线的定义可得∠PBN=2∠DBN,即可得∠APB=2∠ADB;(3)由AD∥BN,根据两直线平行,内错角相等即可得∠ACB=∠CBN;又∠ACB=∠ABD,可得∠CBN=∠ABD,所以∠ABC=∠DBN;
∠ABN=60°;(2)不变化,∠APB=2∠ADB,已知AM∥BN,根据两直线平行,内错角相等即可得∠APB=∠PBN,∠ADB=∠DBN;由BD平分∠PBN,根据角平分线的定义可得∠PBN=2∠DBN,即可得∠APB=2∠ADB;(3)由AD∥BN,根据两直线平行,内错角相等即可得∠ACB=∠CBN;又∠ACB=∠ABD,可得∠CBN=∠ABD,所以∠ABC=∠DBN;
由(1)可得,∠CBD=60°,∠ABN=120°,即可求得∠ABC=![]() (120°﹣60°)=30°.
(120°﹣60°)=30°.
试题解析:
(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∵∠A=60°,
∴∠ABN=120°,
∵BC、BD分别平分∠ABP和∠PBN,
∴∠CBP=![]() ∠ABP,∠DBP=
∠ABP,∠DBP=![]() ∠NBP,
∠NBP,
∴∠CBD=![]() ∠ABN=60°;
∠ABN=60°;
(2)不变化,∠APB=2∠ADB,
证明:∵AM∥BN,
∴∠APB=∠PBN,
∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN,
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=![]() (120°﹣60°)=30°,
(120°﹣60°)=30°,
故答案为:30°.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】已知a=3.50是由四舍五入得到的近似数,则a的可能取值范围是( )
A. 3.45≤a<3.55 B. 3.495≤a<3.505
C. 3.495≤a≤3.505 D. 3.49 5<a<3.505
查看答案和解析>>
科目:初中数学 来源: 题型:
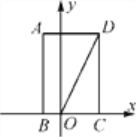
【题目】如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2![]() ,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是
,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是
A. (–![]() ,1) B. (–1,
,1) B. (–1,![]() ) C. (–1,
) C. (–1,![]() )或(1,–
)或(1,–![]() ) D. (–
) D. (–![]() ,1)或(1,–
,1)或(1,–![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便相距2 km的A,B两处居民区的交往,修筑一条笔直的公路(即图中的线段AB),经测量,在A处的北偏东60°方向、B处北偏西45°方向的C处有一半径为0.7 km的圆形公园,问计划修筑的公路会不会穿过公园?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2.
﹣2.
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知:x是3+![]() 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生由于看错了运算符号,把一个整式A减去多项式ab-2bc+3ac误认为加上这个多项式,结果得出的答案是2bc-3ac+2ab.
(1)求整式A;
(2)求原题的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2018届本科生的就业情况,某网站对2018届本科生的签约状况进行了网络调查,至4月底,参与网络调查的12000人中,只有4320人已与用人单位签约在这个调查中,样本容量是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com