
【题目】某校举行全市读书活动月演讲比赛的选拔赛,根据选拔赛成绩拟从小红和小王两位同学中推选1人参加全市的总决赛,两人的选拔赛成绩如下(单位:分):
形象 | 主题 | 普通话 | 演讲技巧 | |
小红 | 85 | 70 | 80 | 85 |
小王 | 95 | 70 | 75 | 80 |
(1)若要按形象占40%,主题占10%,普通话占20%,演讲技巧占30%计算总分,哪位选手将胜出?
(2)评委们已算出小红和小王同学的形象、主题、普通话、演讲技巧四项成绩的平均分都是80分,小红的成绩方差为![]() ,请你计算小王成绩的方差,并说明若要选派各方面素质均衡的选手参赛,哪位选手将胜出?
,请你计算小王成绩的方差,并说明若要选派各方面素质均衡的选手参赛,哪位选手将胜出?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(探究活动)
如图1:已知直线a与b平行,直线c与直线a、b分别相交于点A. B,直线d与直线a、b分别相交于点C. D,点P在直线c上移动,连接PC、PD.探究∠CPD、∠PCA、∠PDB之间的数量关系.
(探究过程)
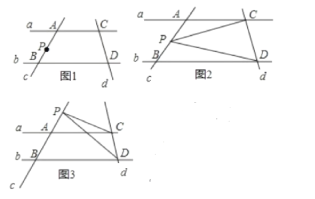
(1)当点P在点A. B之间移动时,如图2,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
(2)当点P在A. B两点外移动时,如图3,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 上一点,
上一点,![]() 于
于![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
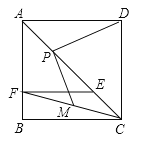
(1)求证:![]() ;
;
(2)当点![]() 在对角线
在对角线![]() (不含
(不含![]() 、
、![]() 两点)上运动时,
两点)上运动时,![]() 是否为定值?如果是,请求其值;如果不是,试说明理由.
是否为定值?如果是,请求其值;如果不是,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
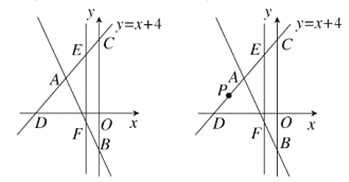
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点D、C,直线AB与
轴分别交于点D、C,直线AB与![]() 轴交于点
轴交于点![]() ,与直线CD交于点
,与直线CD交于点![]() .
.
(1)求直线AB的解析式;
(2)点E是射线CD上一动点,过点E作![]() 轴,交直线AB于点F,若以
轴,交直线AB于点F,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请求出点E的坐标;
为顶点的四边形是平行四边形,请求出点E的坐标;
(3)设P是射线CD上一动点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出符合条件的点Q的个数及其中一个点Q的坐标;否则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,OC平分∠AOB,在直线AB另一端以O为顶点作∠DOE=900。

(1) 若∠AOE=480,求∠BOD的度数。
(2) 写出图中与∠AOE互余的角。
(3) ∠AOE与∠COD有什么数量关系,请写出你的结论并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
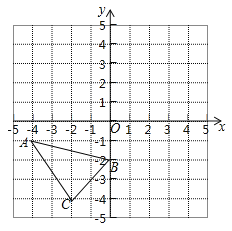
【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两种型号的空调,已知购进3台A型号空调和5台B型号空调共用14500元;购进4台A型号空调和10台B型号空调共用25000元.
(1)求A,B两种型号空调的进价;
(2)若超市准备用不超过54000元的资金再购进这两种型号的空调共30台,求最多能购进A种型号的空调多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
假设月销售件数为x,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com