
【题目】如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 上一点,
上一点,![]() 于
于![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
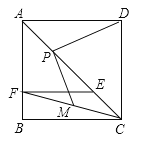
(1)求证:![]() ;
;
(2)当点![]() 在对角线
在对角线![]() (不含
(不含![]() 、
、![]() 两点)上运动时,
两点)上运动时,![]() 是否为定值?如果是,请求其值;如果不是,试说明理由.
是否为定值?如果是,请求其值;如果不是,试说明理由.
【答案】(1)证明见解析;(2)是定值,![]()
【解析】
(1)首先证明△AFE是等腰直角三角形,可得PF⊥AE,由直角三角形的性质可得结论;
(2)由“SAS”可证△APB≌△APD,可得PB=PD,通过证明△AFC∽△APB,可得![]() ,即可得
,即可得![]() .
.
解:(1)如图,连接PF,
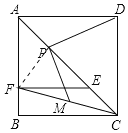
∵四边形ABCD是正方形
∴∠BAC=45°=∠CAD,AB=AD
∵EF⊥AB
∴∠BAC=∠AEF=45°
∴AF=EF,
∴△AFE是等腰直角三角形,且P是AE中点,
∴PF⊥AE,
∵点M是Rt△PFC斜边FC的中点
∴PM=![]() FC
FC
(2)是定值,
理由如下:如图,连接PB
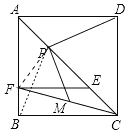
∵AP=AP,∠BAC=∠DAC=45°,AB=AD
∴△APB≌△APD(SAS)
∴PD=PB
∵△ABC,△AFE是等腰直角三角形
∴![]() ,
,![]()
∴![]() ,且∠BAP=∠FAC
,且∠BAP=∠FAC
∴△AFC∽△APB
∴![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图所示,梯形AOCD中,AD=9,OC=10,AO=4,在线段OC上任取一点N(不与O,C重合),连接DN,作NE⊥DN,交AO于点E.

(1)当CN=2时,求点E的坐标.
(2)若CN=x,OE=y,求y与x的函数关系式.
(3)探索与研究:若点M从O点沿OC方向、N点从C点沿CO方向同时等速运动,现有一点F,满足MF⊥MN,NF⊥ND.
①猜想F点在什么线上运动?并求出这条线所对应的函数关系式,并写出自变量的取值范围;
②求出F点在运动过程中的最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.
(1)求从布袋中摸出一个球是红球的概率;
(2)现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是![]() ,问取走了多少个白球?
,问取走了多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)共随机调查了___名学生,课外阅读时间在68小时之间有___人,并补全频数分布直方图;
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)请估计该校3000名学生每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全市读书活动月演讲比赛的选拔赛,根据选拔赛成绩拟从小红和小王两位同学中推选1人参加全市的总决赛,两人的选拔赛成绩如下(单位:分):
形象 | 主题 | 普通话 | 演讲技巧 | |
小红 | 85 | 70 | 80 | 85 |
小王 | 95 | 70 | 75 | 80 |
(1)若要按形象占40%,主题占10%,普通话占20%,演讲技巧占30%计算总分,哪位选手将胜出?
(2)评委们已算出小红和小王同学的形象、主题、普通话、演讲技巧四项成绩的平均分都是80分,小红的成绩方差为![]() ,请你计算小王成绩的方差,并说明若要选派各方面素质均衡的选手参赛,哪位选手将胜出?
,请你计算小王成绩的方差,并说明若要选派各方面素质均衡的选手参赛,哪位选手将胜出?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长都相等,三角形ABC的三个顶点都在格点(小正方形的顶点)上.
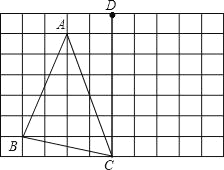
(1)平移三角形ABC,使顶点A平移到点D的位置,得到三角形DEF,请在图中画出三角形DEF;(注:点B的对应点为点E)
(2)若∠A=50°,则直线AC与直线DE相交所得锐角的度数为 °,依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com