
 有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?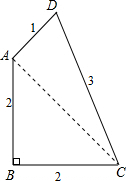 解:都是直角三角形.理由如下:
解:都是直角三角形.理由如下:

 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
| 2 |
| a-1 |
| a+3 |
| 1-a2 |
| 解答过程 | 解答步骤说明 | 解题依据(用文字或符号填写知识的名称 和具体内容,每空一个 | ||||||||
| 此处不填 | 此处不填 | ||||||||
=
| 示例通分 | 示例:分式的基本性质:分式的分子和分母都乘以同一个不等于领的整式,分式的值不变(或者“同分母分式相加减法则:
| ||||||||
=
| 去括号 | | ||||||||
=
| 合并同类项 | 此处不填 | ||||||||
| = | ③ | |
查看答案和解析>>
科目:初中数学 来源: 题型:
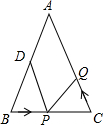 如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.
如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.| A、3 | ||
B、
| ||
| C、3或3.75 | ||
| D、2或3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
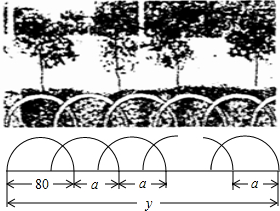 如图,某花园护栏是用直径为80厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加a厘米(a>0).设半圆形条钢的总个数为x(x为正整数),护栏总长度为y厘米.
如图,某花园护栏是用直径为80厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加a厘米(a>0).设半圆形条钢的总个数为x(x为正整数),护栏总长度为y厘米.查看答案和解析>>
科目:初中数学 来源: 题型:
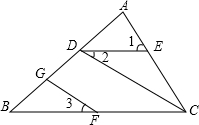 已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.
已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y=(x+1)2-2 |
| B、y=(x+1)2 |
| C、y=(x+1)2-4 |
| D、y=(x+1)2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com