
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
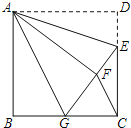
(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
【答案】(1)见解析;(2)3.6
【解析】
试题分析:(1)①利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;
②利用勾股定理得出GE2=CG2+CE2,进而求出BG即可;
(2)首先过C作CM⊥GF于M,由勾股定理以及由面积法得,CM=2.4,进而得出答案
解:(1)①在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴△ABG≌△AFG(HL);
②∵CD=3DE
∴DE=2,CE=4,
设BG=x,则CG=6﹣x,GE=x+2
∵GE2=CG2+CE2
∴(x+2)2=(6﹣x)2+42,
解得x=3,
∴CG=6﹣3=3;
(2)如图,过C作CM⊥GF于M,
∵BG=GF=3,
∴CG=3,EC=6﹣2=4,
∴GE=![]() =5,
=5,
CMGE=GCEC,
∴CM×5=3×4,
∴CM=2.4,
∴S△FGC=![]() GF×CM=
GF×CM=![]() ×3×2.4=3.6.
×3×2.4=3.6.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点(不与A,B重合),且CD切⊙O于点D.
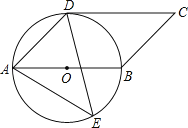
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求:△ADE面积的最大值.
cm,试求:△ADE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b互为相反数,b、c互为倒数,并且m的立方等于它本身.
(1)试求![]() +ac值;
+ac值;
(2)若a>1,b<﹣1,且m<0,S=|2a一3b|﹣2|b﹣m|﹣|b+![]() |,试求4(2a一S)+2(2a﹣S)﹣(2a﹣S)的值.
|,试求4(2a一S)+2(2a﹣S)﹣(2a﹣S)的值.
(3)若m≠0,当x为有理数时,|x+m|﹣|x﹣m|存在最大值,请求出这个最大值(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】演唱比赛,7位评委给1号选手的评分如下:9.3,8.9,9.2,9.4,9.2,9.7,9.4,规定去掉一个最高分和一个最低分,剩余得分的平均数作选手的最后得分.那么,1号选手的最后得分是________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
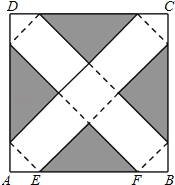
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com