
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
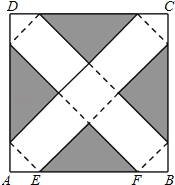
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
【答案】(1)这个包装盒的体积是432![]() cm3;
cm3;
(2)当x=8时,S取得最大值384cm2.
【解析】
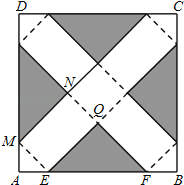
试题分析:(1)根据已知得出这个正方体的底面边长NQ=ME=![]() x,EF=
x,EF=![]() ME=2x,再利用AB=24cm,求出x即可得出这个包装盒的体积V;
ME=2x,再利用AB=24cm,求出x即可得出这个包装盒的体积V;
(2)利用已知表示出包装盒的表面,进而利用函数最值求出即可.
解:(1)根据题意,设AE=BF=x(cm),折成的包装盒恰好是个正方体,
知这个正方体的底面边长NQ=ME=![]() x,则QE=QF=
x,则QE=QF=![]() x,故EF=
x,故EF=![]() ME=2x,
ME=2x,
∵正方形纸片ABCD边长为24cm,
∴x+2x+x=24,
解得:x=6,
则 正方体的底面边长a=6![]() ,
,
V=a3=![]() =432
=432![]() (cm3);
(cm3);
答:这个包装盒的体积是432![]() cm3;
cm3;
(2)设包装盒的底面边长为acm,高为hcm,则a=![]() ,h=
,h=![]() ,
,
∴S=4ah+a2=4![]() x
x![]() (12﹣x)+
(12﹣x)+![]() =﹣6x2+96x=﹣6(x﹣8)2+384,
=﹣6x2+96x=﹣6(x﹣8)2+384,
∵0<x<12,
∴当x=8时,S取得最大值384cm2.


科目:初中数学 来源: 题型:
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2014次“移位”后,他到达编号为 的点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
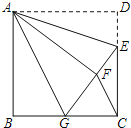
(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据:20、30、40、50、50、50、60、70、80,其中平均数、中位数、众数的大小关系是( )
A.平均数>中位数>众数 B.平均数<中位数<众数
C.中位数<众数<平均数 D.平均数=中位数=众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种“24点”游戏,其游戏规则是这样的,将4个1~13之间的数,进行加减乘除四则运算(每个数且只能用一次),使运算结果为24,例如,1,2,3,4可作如下运算:(1+2+3)×4=24,1×2×3×4=24.现有四个有理数3,4,﹣6,10,你能运用上述规则,写出一种运算式,使其结果等于24.你写出算式是:_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com