
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点(不与A,B重合),且CD切⊙O于点D.
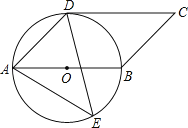
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求:△ADE面积的最大值.
cm,试求:△ADE面积的最大值.
【答案】(1)∠AED的度数为45 或135;
(2)(![]() )cm 2.
)cm 2.
【解析】
试题分析:(1)利用平行四边形的性质以及切线的性质和圆周角定理求出即可;
(2)利用当三角形高度最大时面积最大,求出EF的长即可得出答案.
解:(1)连接DO,DB,
∵四边形ABCD是平行四边形,CD切⊙O于点D.
∴DO⊥DC,
∴∠DBA=45°,
∵∠DBA=∠E,
∴∠E=45°,
当E′点在如图所示位置,即可得出∠AE′D=180°﹣45°=135°,
∴∠AED的度数为45 或135;
(2)当∠AED=45°,且E在AD垂直平分线上时,△ADE的面积最大,
∵∠AED=45°,
∴∠DAB=∠DBA=45°,∠ADB=90°,
∵⊙O的半径为![]() cm,
cm,
∴AB=6![]() cm,
cm,
∴AD=DB=6,
AF=FO=3,
∴S△ADE=![]() ×AD×(FO+EO)=
×AD×(FO+EO)=![]() ×6×(3+3
×6×(3+3![]() )=(
)=(![]() )cm 2.
)cm 2.




 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A. 0.51×109 B. 5.1×108 C. 5.1×109 D. 51×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着微电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.0000007(平方毫米),这个数用科学记数法表示为( )
A.7×10﹣6
B.0.7×10﹣6
C.7×10﹣7
D.70×10﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2014次“移位”后,他到达编号为 的点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
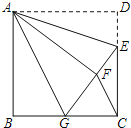
(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com