
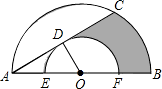
 如图,AB是半圆O的直径,以O为圆心,OE长为半径的小半圆交AB于E,F两点,弦AC是小半圆的切线,D为切点,已知,AO=4,AC=4
如图,AB是半圆O的直径,以O为圆心,OE长为半径的小半圆交AB于E,F两点,弦AC是小半圆的切线,D为切点,已知,AO=4,AC=4 ,则图中阴影部分的面积等于________.
,则图中阴影部分的面积等于________.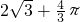
 ,由勾股定理求出OD=2=
,由勾股定理求出OD=2= AO,求出∠A=30°=∠ACO,∠AOD=60°,⊙AOC=120°,∠COB=60°,分别求出扇形AOC的面积、△AOC的面积、扇形DOF的面积、△ADO的面积、大半圆的面积,代入阴影部分的面积(S大半圆-(S扇形AOC-S△AOC)-S△ADO-S扇形DOF)求出即可.
AO,求出∠A=30°=∠ACO,∠AOD=60°,⊙AOC=120°,∠COB=60°,分别求出扇形AOC的面积、△AOC的面积、扇形DOF的面积、△ADO的面积、大半圆的面积,代入阴影部分的面积(S大半圆-(S扇形AOC-S△AOC)-S△ADO-S扇形DOF)求出即可.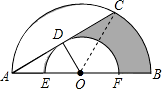
 ,
, AO,
AO,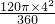 =
= π,
π, ×AC×OD=
×AC×OD= ×4
×4 ×2=4
×2=4 ,
, =
= π,
π, ×AD×OD=2
×AD×OD=2 ,
, π×42=16π,
π×42=16π, π-4
π-4 )-2
)-2 -
- π
π +
+ π.
π. +
+ π.
π.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=| 1 |
| 2 |
 |
| AC |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com