
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )

A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
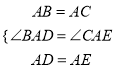 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,本选项正确;
②∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,本选项正确;
③∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵∠ABD=∠ACE
∴∠ACE+∠DBC=45°,本选项正确;
④∵∠ABD=∠ACE,
∴只有当∠ABD=∠DBC时,∠ACE=∠DBC才成立。
综上所述,正确的结论有3个.
故选:B.


科目:初中数学 来源: 题型:
【题目】甲乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做抽数字游戏,游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,抽出的牌不放回,然后将剩下的牌洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数,若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请利用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装销售商在进行市场占有率的调查时,他最应该关注的是……………( )
A. 服装型号的平均数 B. 服装型号的众数
C. 服装型号的中位数 D. 最小的服装型号
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店在开学初用2000元购进一批学生书包,按每个120元出售,很快销售一空,于是商店又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元,仍按120元出售,最后剩下4个按八折卖出,这笔生意该店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球 ![]() 沿从
沿从 ![]() 到
到 ![]() 方向在
方向在 ![]() 点处撞击
点处撞击 ![]() 边后将沿从
边后将沿从 ![]() 到
到 ![]() 方向反弹,根据反弹原则可知
方向反弹,根据反弹原则可知 ![]() ,即
,即 ![]() .如图(2)和(3),
.如图(2)和(3),![]() 是一个长方形的弹子球台面,有黑白两球
是一个长方形的弹子球台面,有黑白两球 ![]() 和
和 ![]() ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)

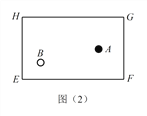

(1)探究(1):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]() 经台边
经台边 ![]() 反弹一次后撞击到白球
反弹一次后撞击到白球 ![]() ?请在图(2)中画出黑球
?请在图(2)中画出黑球 ![]() 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
(2)探究(2):黑球 ![]() 沿直线撞击台边
沿直线撞击台边 ![]() 哪一点时,可以使黑球
哪一点时,可以使黑球 ![]()
![]() 反弹一次后,再撞击台边
反弹一次后,再撞击台边 ![]() 反弹一次撞击到白球
反弹一次撞击到白球 ![]() ?请在图(3)中画出黑球
?请在图(3)中画出黑球 ![]() 的路线图,标出黑球撞击
的路线图,标出黑球撞击 ![]() 边的撞击点,简单说明作法,不用证明.
边的撞击点,简单说明作法,不用证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com