
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
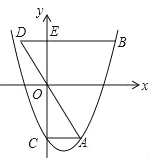
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
【答案】(1)2m;(2)落在抛物线上;(3)①、m=![]() ;②、m=
;②、m=![]()
【解析】
试题分析:(1)根据A、C两点纵坐标相同,求出点A横坐标即可解决问题;(2)求出点D坐标,然后判断即可;(3)①首先根据EO=2FG,证明BG=2DE,列出方程即可解决问题;②求出直线AE、BO的解析式,求出交点M的横坐标,列出方程即可解决问题.
试题解析:(1)∵C(0,﹣3),AC⊥OC, ∴点A纵坐标为-3, y=-3时 -3=x2﹣mx-3,解得x=0或m,
∴点A坐标(m,﹣3), ∴AC=m, ∴BE=2AC=2m.
(2)∵m=![]() , ∴点A坐标(
, ∴点A坐标(![]() ,﹣3), ∴直线OA为y=﹣
,﹣3), ∴直线OA为y=﹣![]() x, ∴抛物线解析式为y=x2﹣
x, ∴抛物线解析式为y=x2﹣![]() x﹣3,
x﹣3,
∴点B坐标(2![]() ,3), ∴点D纵坐标为3, 对于函数y=﹣
,3), ∴点D纵坐标为3, 对于函数y=﹣![]() x,当y=3时,x=﹣
x,当y=3时,x=﹣![]() ,
,
∴点D坐标(﹣![]() ,3). ∵对于函数y=x2﹣
,3). ∵对于函数y=x2﹣![]() x﹣3,x=﹣
x﹣3,x=﹣![]() 时,y=3,
时,y=3,
∴点D在落在抛物线上.
(3)①∵∠ACE=∠CEG=∠EGA=90°, ∴四边形ECAG是矩形, ∴EG=AC=BG, ∵FG∥OE,
∴OF=FB,∵EG=BG, ∴EO=2FG, ∵![]() DEEO=
DEEO=![]() GBGF, ∴BG=2DE, ∵DE∥AC, ∴
GBGF, ∴BG=2DE, ∵DE∥AC, ∴![]() =
=![]() =
=![]() ,
,
∵点B坐标(2m,2m2﹣3), ∴OC=2OE, ∴3=2(2m2﹣3),∵m>0, ∴m=![]() .
.
②∵A(m,﹣3),B(2m,2m2﹣3),E(0,2m2﹣3),
∴直线AE解析式为y=﹣2mx+2m2﹣3,直线OB解析式为y=![]()
![]() x,
x,
由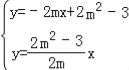 消去y得到﹣2mx+2m2﹣3=
消去y得到﹣2mx+2m2﹣3=![]() x,解得x=
x,解得x=![]() ,
,
∴点M横坐标为![]() , ∵△AMF的面积=△BFG的面积,
, ∵△AMF的面积=△BFG的面积,
∴![]() (
(![]() +3)(m﹣
+3)(m﹣![]() )=
)=![]() m
m![]() (2m2﹣3), 整理得到:2m4﹣9m2=0, ∵m>0,
(2m2﹣3), 整理得到:2m4﹣9m2=0, ∵m>0,
∴m=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列因式分解错误的是( )
A. 2x(x﹣2)+(2﹣x)=(x﹣2)(2x+1) B. x2+2x+1=(x+1)2
C. x2y﹣xy2=xy(x﹣y) D. x2﹣y2=(x+y)(x﹣y)
查看答案和解析>>
科目:初中数学 来源: 题型:
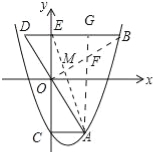
【题目】(1)将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 ,∠CAC′= °.

(2)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
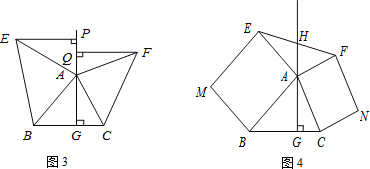
(3)如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点E(﹣4,2),点F(﹣1,﹣1),以点O为位似中心,按比例1:2把△EFO缩小,则点E的对应点E的坐标为( )
A. (2,﹣1)或(﹣2,1) B. (8,﹣4)或(﹣8,4) C. (2,﹣1) D. (8,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)
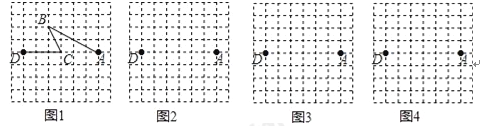
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0,如果AB=3,AO=2,那么AC的长等于______.
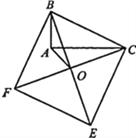
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com