
【题目】如图一座拱桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.、
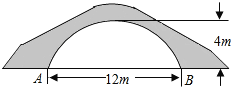
(1)建立平面直角坐标系,并求该抛物线的函数表达式;
(2)若水面上升1m,水面宽度将减少多少?
【答案】(1)图见解析,抛物线的函数表达式为![]() (注:因建立的平面直角坐标系的不同而不同);(2)
(注:因建立的平面直角坐标系的不同而不同);(2)![]()
【解析】
(1)以AB的中点为平面直角坐标系的原点O,AB所在线为x轴,过点O作AB的垂线为y轴建立平面直角坐标系(图见解析);因此,抛物线的顶点坐标为![]() ,可设抛物线的函数表达式为
,可设抛物线的函数表达式为![]() ,再将B点的坐标
,再将B点的坐标![]() 代入即可求解;
代入即可求解;
(2)根据题(1)的结果,令![]() 求出x的两个值,从而可得水面上升1m后的水面宽度,再与12m作差即可得出答案.
求出x的两个值,从而可得水面上升1m后的水面宽度,再与12m作差即可得出答案.
(1)以AB的中点为平面直角坐标系的原点O,AB所在线为x轴,过点O作AB的垂线为y轴,建立的平面直角坐标系如下:
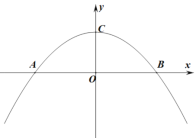
根据所建立的平面直角坐标系可知,B点的坐标为![]() ,抛物线的顶点坐标为
,抛物线的顶点坐标为![]()
因此设抛物线的函数表达式为![]()
将![]() 代入得:
代入得:![]()
解得:![]()
则所求的抛物线的函数表达式为![]() (注:因建立的平面直角坐标系的不同而不同);
(注:因建立的平面直角坐标系的不同而不同);
(2)由题意,令![]() 得
得![]()
解得:![]()
则水面上升1m后的水面宽度为:![]() (米)
(米)
故水面上升1m,水面宽度将减少![]() 米.
米.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
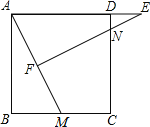
【题目】如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:![]() .
.
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2.

(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= ,OC△OA= ;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
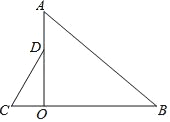
【题目】如图,△AOB和△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在OA上.将△COD绕点O顺时针旋转一周,在旋转过程中,当旋转角是_____°时,CD∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2,并指出她与嘉嘉抽到勾股数的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
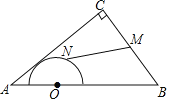
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形硬纸片ABCD的顶点A在![]() 轴的正半轴及原点上滑动,顶点B在
轴的正半轴及原点上滑动,顶点B在![]() 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为
轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为![]() ,其中正确的结论是_________(填写序号).
,其中正确的结论是_________(填写序号).
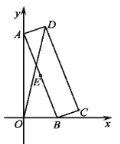
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
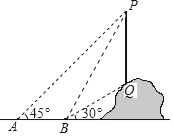
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把菱形![]() 向右平移至
向右平移至![]() 的位置,作
的位置,作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() :④
:④![]() .
.
则其中所有成立的结论是( )
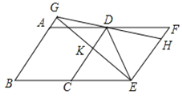
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com