
����Ŀ�����ǹ涨���������������ߵġ�����ֵ�����ڵ������ϵ����ߺ����һ���ƽ�����ͼ1���ڡ�ABC�У�AO��BC���ϵ����ߣ�AB��AC�ġ�����ֵ���͵���AO2��BO2��ֵ���ɼ�ΪAB��AC=AO2��BO2��

��1����ͼ1�У�����BAC=90�㣬AB=8��AC=6��AO��BC���ϵ����ߣ���AB��AC= ��OC��OA= ��
��2����ͼ2���ڡ�ABC�У�AB=AC=4����BAC=120�㣬��AB��AC��BA��BC��ֵ��
��3����ͼ3���ڡ�ABC�У�AB=AC��AO��BC���ϵ����ߣ���N��AO�ϣ���ON=![]() AO����֪AB��AC=14��BN��BA=10�����ABC�������
AO����֪AB��AC=14��BN��BA=10�����ABC�������
���𰸡���1��0��7����2����8��24����3��![]() ��
��
�������������������1�����ȸ��ݹ��ɶ������BC=10��������ֱ�������ε����ʵó�OA=OB=OC=5����������¶��弴�ɵó����ۣ�
�����õ��������ε��������CD=3�������ù��ɶ������OD��������¶��弴�ɵó����ۣ�
��2���������ú�30���ֱ�������ε��������AO=2��OB=![]() �������¶��弴�ɵó����ۣ�
�������¶��弴�ɵó����ۣ�
���ȹ���ֱ�����������BE��AE�����ù��ɶ������BD��������¶��弴�ɵó����ۣ�
��3���ȹ���ֱ�������Σ�������OA��BD2��������¶��彨����������⼴�ɵó����ۣ�
�����������1���١ߡ�BAC=90�㣬AB=8��AC=6����BC=10��
�ߵ�O��BC���е㣬��OA=OB=OC=![]() BC=5����AB��AC=AO2��BO2=25��25=0��
BC=5����AB��AC=AO2��BO2=25��25=0��
����ͼ1��ȡAC���е�D������OD����CD=![]() AC=3��
AC=3��
��OA=OC=5����OD��AC��
��Rt��COD��OD=![]() =4����OC��OA=OD2��CD2=16��9=7��
=4����OC��OA=OD2��CD2=16��9=7��
�ʴ�Ϊ��0��7��
��2������ͼ2��ȡBC���е�D������AO����AB=AC����AO��BC��
�ڡ�ABC�У�AB=AC����BAC=120�㣬���ABC=30�㣬
��Rt��AOB�У�AB=4����ABC=30�㣬��AO=2��OB=![]() ��
��
��AB��AC=AO2��BO2=4��12=��8��
��ȡAC���е�D������BD����AD=CD=![]() AC=2������B��BE��AC��CA���ӳ�����E����Rt��ABE�У���BAE=180�㩁��BAC=60�㣬���ABE=30�㣬
AC=2������B��BE��AC��CA���ӳ�����E����Rt��ABE�У���BAE=180�㩁��BAC=60�㣬���ABE=30�㣬
��AB=4����AE=2��BE=![]() ����DE=AD+AE=4��
����DE=AD+AE=4��
��Rt��BED�У����ݹ��ɶ����ã�BD=![]() =
=![]() =
=![]() ��
��
��BA��BC=BD2��CD2=24��
��3����ͼ3����ON=x��OB=OC=y����BC=2y��OA=3x��
��AB��AC=14����OA2��OB2=14����9x2��y2=14�٣�
ȡAN���е�D������BD����AD=DB=![]() AN=
AN=![]() ��
��![]() OA=ON=x����OD=ON+DN=2x��
OA=ON=x����OD=ON+DN=2x��
��Rt��BOD��BD2=OB2+OD2=y2+4x2����BN��BA=10��
��BD2��DN2=10����y2+4x2��x2=10����3x2+y2=10��
�����٢ڵã� 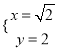 ��
��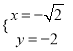 ���ᣩ����BC=4��OA=
���ᣩ����BC=4��OA=![]() ����S��ABC=
����S��ABC=![]() BC��AO=
BC��AO=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC��AC��BC=8��AC=6��AB=10����� C ���߶� AB �ľ�����_____��
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835434496/STEM/46ca9c8351da4594816ea507a60c9cdd.png]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��

��1�������1����B����ô_______��_______��������__________________________��
��2�������3����D����ô_______��_______��������__________________________��
��3�����ҪʹBE��DF�������1����_______��������_________________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4����P��AB���ϵ�һ�����㣬����CP������P��PC�Ĵ��߽�AD�ڵ�E���� PEΪ����������PEFG������G���߶�PC�ϣ��Խ���EG��PF�ཻ�ڵ�O��
��1����AP=1����AE= ��
��2������֤����Oһ���ڡ�APE�����Բ�ϣ�
�ڵ���P�ӵ�A�˶�����Bʱ����OҲ��֮�˶������O������·������
��3���ڵ�P�ӵ�A����B���˶������У���APE�����Բ��Բ��Ҳ��֮�˶������Բ�ĵ�AB�ߵľ�������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
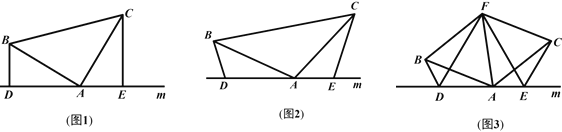
����Ŀ����1����ͼ1����֪������ABC�У���BAC=90�㣬AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E��֤����DE��BD+CE��
��2����ͼ2������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ����ҡ�BDA����AEC����BAC������������Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ�������������������֤����������������˵�����ɣ�
��3����չ��Ӧ�ã���ͼ3��D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E����
�����غϣ�����FΪ��BACƽ�����ϵ�һ�㣬����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE������BDA����AEC����BAC�����ж���DEF����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������У������������( )
A.��ȵĽ��ǶԶ���
B.ͬ���ڽǻ���
C.��һ�㲻ֻ��һ��ֱ������ֱ֪�ߴ�ֱ
D.����ֱ�� a��b��c����� b��a��c��a����ô b��c
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com