
����Ŀ�������ű��ΪA��B��C��D�Ŀ�Ƭ��������⣬������ȫ��ͬ��������ֱ�д����ͼ��ʾ���������������ϣ�ϴ�ȷźã�
��1������֪��������a2+b2=c2������������a��b��c��Ϊ���������μδ��������ȡһ�ţ���鵽�Ŀ�Ƭ�ϵ����ǹ������ĸ���P1��
��2���������������ȡһ�ţ����Żأ����ٴ�ʣ�µĿ�Ƭ�������ȡһ�ţ���Ƭ��A��B��C��D��ʾ���������б�������ͼ�ķ�����鵽�����ſ�Ƭ�ϵ������ǹ������ĸ���P2����ָ������μγ鵽�������Ŀ�����һ����

���𰸡���1��![]() ����2������μγ鵽�������Ŀ����Բ�һ����
����2������μγ鵽�������Ŀ����Բ�һ����
�����������������
��1�����ݵȿ����¼��ĸ��ʵĶ��壬�ֱ�ȷ���ܵĿ����Ժ��ǹ�����������ĸ�����
��2�����б����оٳ����е���������ſ�Ƭ�ϵ������ǹ��������������.
���������
��1���μ������ȡһ�ſ�Ƭ������4�ֵȿ��ܽ�������г鵽�Ŀ�Ƭ�ϵ����ǹ������Ľ����3�֣����Լμγ�ȡһ�ſ�Ƭ�ϵ����ǹ������ĸ���P1=![]() ��
��
��2�������
A | B | C | D | |
A | ��A��B�� | ��A��C�� | ��A��D�� | |
B | ��B��A�� | ��B��C�� | ��B��D�� | |
C | ��C��A�� | ��C��B�� | ��C��D�� | |
D | ��D��A�� | ��D��B�� | ��D��C�� |
���б���֪�����γ�ȡ��Ƭ�����п��ܳ��ֵĽ����12�֣����г鵽�����ſ�Ƭ�ϵ������ǹ���������6�֣�
��P2=![]() ��
��
��P1=![]() ��P2=
��P2=![]() ��P1��P2
��P1��P2
������μγ鵽�������Ŀ����Բ�һ����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ������⣺����֪��������n���εĶԽ���������ʽΪ�� ![]() n��n��3����
n��n��3����
���һ��n���ι���20���Խ��ߣ���ô���Եõ�����![]() n��n��3��=20 ��
n��n��3��=20 ��
������n2��3n��40=0�����n=8��n=��5
��nΪ���ڵ���3����������n=��5�������⣬��ȥ��
��n=8����������ǰ˱��Σ�
�����������ݣ��ʣ�
��1����һ������ι���14���Խ��ߣ����������εı�����
��2��Aͬѧ˵���������һ������ι���10���Խ�����������ΪAͬѧ˵����ȷ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����12Ԫ������ʼDZ���С����21Ԫ��Ӳ��ʼDZ���
��1����֪ÿ��Ӳ��ʼDZ�������ʼDZ���1.2Ԫ��С����С��������ͬ�����ıʼDZ���
��2����֪ÿ��Ӳ��ʼDZ�������ʼDZ���aԪ���Ƿ����������a��ʹ��ÿ��Ӳ��ʼDZ�������ʼDZ��ļ۸���������������С����С��������ͬ�����ıʼDZ��������ڣ����a��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Rt��ACB����ACB��90�㣬AC��BC����A��C�ֱ���x�ᡢy����������ϣ�

��1����ͼ1����֤����BCO����CAO
��2����ͼ2����OA��5��OC��2����B�������
��3����ͼ3����C��0��3����Q��A�������x���ϣ���S��CQA��18���ֱ���AC��CQΪ���ڵ�һ���ڶ�����������Rt��CAN������Rt��QCM������MN��y����P�㣬OP�ij����Ƿ����ı䣿�����䣬���OP��ֵ�����仯����OP��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ��x����A����1��0����B��2��0������y����C��0����2������A��C��ֱ�ߣ�
��1������κ����Ľ���ʽ��
��2����P��x���������ϣ���PA=PC����OP�ij���
��3����M�ڶ��κ���ͼ���ϣ���MΪԲ�ĵ�Բ��ֱ��AC���У��е�ΪH��
����M��y���Ҳ࣬�ҡ�CHM�ס�AOC����C���A��Ӧ�������M�����ꣻ
������M�İ뾶Ϊ![]() �����M�����꣮
�����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��x����A��B���㣬��y���ڵ�C,��֪�����ߵĶԳ���Ϊx=1��B(3,0),C(0,-3)��
��1������κ���y=ax2+bx+c�Ľ���ʽ��
��2���������߶Գ������Ƿ����һ��P��ʹ��P��B��C�������֮����������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
��3��ƽ����x���һ��ֱ�߽���������M,N���㣬����MNΪֱ����Բǡ����x�����У����Բ�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����ƽ���ı��ε������(�ױ�)��(�����ױ��ϵĸ�)����ͼ���ı���ABCD����ƽ���ı��Σ�AD��BC��AB��CD�����������ΪS��
��1����ͼ�٣���MΪAD������һ�㣬����BCM�����ΪS1����S1��S�� ��
��2����ͼ�ڣ���PΪƽ���ı���ABCD������һ��ʱ������PAB�����ΪS�@����PCD�����ΪS����ƽ���ı���ABCD�����ΪS�������S�@��S���ĺ���S��������ϵʽΪ ��
��3����ͼ�ۣ���֪��PΪƽ���ı���ABCD������һ�㣬��PAB�����Ϊ3����PBC�����Ϊ7������PBD�������
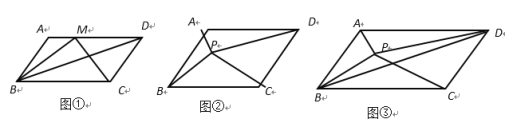
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
�� a 2 ��0�������������ѧ�зdz����ã���ʱ������Ҫ������ʽ�����ȫƽ��ʽ�����磺
x2 4x 5 x2 4x 4 1 x 22 1 ��
�� x 22 ��0��
�� x 22 1 ��1��
�� x2 4x 5 ��1.
���������䷽��������������⣺
(1)��գ� x2 4x 5 ( x )2�� ��
(2)��֪ x2 4x y2 2y 5 0 ���� x y ��ֵ��
(3)�Ƚϴ���ʽ x2 1��2x 3 �Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ж���ȷ���ǣ� ��
A.һ��Խ���ȣ�һ���ڽ���ȵ��ı�����ƽ���ı���
B.һ��Ա�ƽ�У�һ��Խ���ȵ��ı�����ƽ���ı���
C.һ��Ա�ƽ�У���һ��Ա���ȵ��ı�����ƽ���ı���
D.һ��Ա���ȣ�һ��Խ���ȵ��ı�����ƽ���ı���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com