
����Ŀ������ʦ���㹺��װ��ѧУ����һ����ͯ�ڻ�᳡������������Ц���Ͱ������֣���������ļ۸�ͬ����ͬһ���������۸���ͬ�����ڻ᳡������Ҫ�������˵���������ÿ��4������ÿ���۸���ͼ��ʾ�� 
��1����Ц������ĵ�����xԪ�����ú�x�Ĵ���ʽ��ʾ�ڢ������ڢ���������ܼ۸�Ҫ�������ͼ���У�
��2�����ڢ���������ܼ�Ǯ�ȵڢ���������ܼ�Ǯ��2Ԫ�����������������ĵ��ۣ�
���𰸡�
��1���⣺��Ц������ĵ�����xԪ����������ĵ����ǣ�14��3x��Ԫ�����������
�ڢ���������ܼ۸��ǣ�x+3��14��3x��=x+42��9x=42��8x��Ԫ����
�ڢ���������ܼ۸��ǣ�2x+2��14��3x��=2x+28��6x=28��4x��Ԫ��
��2���⣺�������42��8x=28��4x��2��
���x=4��
14��3x=2��
��Ц������ĵ�����4Ԫ����������ĵ�����2Ԫ
����������1����Ц������ĵ�����xԪ���ɵڢ���������ܼ�ǮΪ14Ԫ�ó���������ĵ����ǣ�14��3x��Ԫ������ÿ��������ܼ�Ǯ=Ц������ļ�Ǯ+��������ļ�Ǯ��������ڢ������ڢ���������ܼ۸�2�����ݵڢ���������ܼ�Ǯ�ȵڢ���������ܼ�Ǯ��2Ԫ�г����̣��ⷽ�̼��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȥ������ȷ����(����)
A. x2-(3x-2)=x2-3x-2
B. 7a+(5b-1)=7a+5b+1
C. 2m2-(3m+5)=2m2-3m-5
D. -(a-b)+(ab-1)=a-b+ab-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC����AB=8��CD=2����EC�ij���
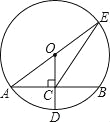
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У���A=50����
��1����ͼ������ABC����ACB�Ľ�ƽ���߽��ڵ�O������BOC= ����
��2����ͼ������ABC����ACB�����ȷ��߷ֱ��Ӧ����O1��O2������BO2C= ����
��3����ͼ������ABC����ACB��n�ȷ��߷ֱ��Ӧ����O1��O2��On��1���ڲ���n��1���㣩������BOn��1C����n�Ĵ���ʽ��ʾ����
��4����ͼ������֪��ABC����ACB��n�ȷ��߷ֱ��Ӧ����O1��O2��On��1������BOn��1C=60������n��ֵ��
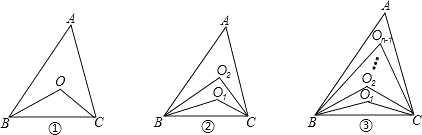
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ξ������·ݹ��Ӵ��ο�25���˴Σ����·ݹ��Ӵ��ο�64���˴Σ���ÿ�µ�ƽ��������Ϊx������з���Ϊ�� ��
A.25��1+x��2=64
B.25+25��1+x��2=64
C.25��1+2x��=64
D.64��1��x2��=25
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и����߶�������������ε��ǣ�������
A. 2cm��3cm��5cm B. 5cm��6cm��10cm
C. 1cm��1cm��3cm D. 3cm��4cm��8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=120�㣬����һ30�Ƚǵ�ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·�����ͼ�С�OMN=30�㣬��NOM=90�㣩 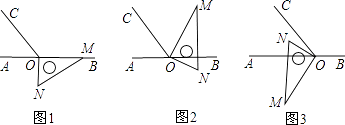
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹOM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC����ֱ��ON�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��6����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC����t��
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ�����̽������AOM���NOC֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵ�������м�������15�ˣ�������Ϊ�˺����ƶ���Ʒ��ÿ���������ͳ������15��ij�µļӹ����������
ÿ�˼ӹ�������� | 540 | 450 | 300 | 240 | 210 | 120 |
���� | 1 | 1 | 2 | 6 | 3 | 2 |
(1)д����15�˸��¼ӹ��������ƽ��������λ����������
(2)���������������˰�ÿλ���˵��¼ӹ����������Ϊ260������Ϊ��������Ƿ������Ϊʲô��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com