
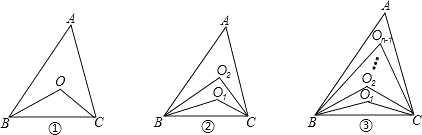
【题目】已知△ABC中,∠A=50°.
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC= °.
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C= °.
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
【答案】(1)、115°;(2)、![]() ;(3)、﹣
;(3)、﹣![]() ×130°;(4)、n=13.
×130°;(4)、n=13.
【解析】
试题分析:(1)、△ABC中,已知∠A即可得到∠ABC与∠ACB的和,而BO、CO是∠ABC,∠ACB的两条角平分线,即可求得∠OBC与∠OCB的度数,根据三角形的内角和定理即可求解;(2)、先根据三角形内角和定理求得∠ABC+∠ACB,再根据三等分线的定义求得∠O2BC+∠O2CB,即可求出∠BO2C;
(3)、先根据三角形内角和定理求得∠ABC+∠ACB,再根据n等分线的定义求得∠On﹣1BC+∠On﹣1CB,即可求出∠BOn﹣1C.(4)、依据(3)的结论即可求出n的值.
试题解析:(1)、∵△ABC中,∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,BO、CO是∠ABC,∠ACB的两条角平分线. ∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB, ∴∠OBC+∠OCB=
∠ACB, ∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=65°,
(∠ABC+∠ACB)=65°,
∴△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=115° (2)、∵点O2是∠ABC与∠ACB的三等分线的交点,
∴∠O2BC+∠O2CB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°=(
×130°=(![]() )°,
)°,
∴∠BO2C=180°﹣(![]() )°=(
)°=(![]() )°.
)°.
(3)、∵点On﹣1是∠ABC与∠ACB的n等分线的交点,
∴∠On﹣1BC+∠On﹣1CB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°, ∴∠BOn﹣1C=180°﹣
×130°, ∴∠BOn﹣1C=180°﹣![]() ×130°;
×130°;
(4)、∵∠BOn﹣1C=60°, ∴180°﹣![]() ×130°=60°,解得n=13.
×130°=60°,解得n=13.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),已知AF平分∠BAC,交边BC于点E,过F作FD⊥BC,若∠B=x°,∠C=(x+36)°,
①∠CAE= (含x的代数式表示)
②求∠F的度数.
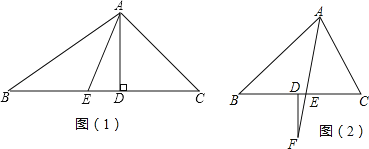
查看答案和解析>>
科目:初中数学 来源: 题型:
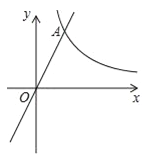
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数![]() 的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
(1)求平移后直线的表达式;
(2)求∠OBC的余切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A. 对重庆市辖区内长江流域水质情况的调查
B. 对乘坐飞机的旅客是否携带违禁物品的调查
C. 对一个社区每天丢弃塑料袋数量的调查
D. 对重庆电视台“天天630”栏目收视率的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小莹自制了一个标靶进行投标比赛,两人各投了10次,如图是他们投标成绩的统计图.
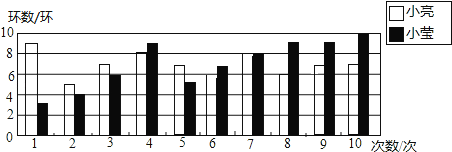
(1)根据图中信息填写下表
平均数 | 中位数 | 众数 | |
小亮 | 7 | ||
小莹 | 7 | 9 |
(2)分别用平均数和中位数解释谁的成绩比较好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com