
【题目】(1)如图(1),已知,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),已知AF平分∠BAC,交边BC于点E,过F作FD⊥BC,若∠B=x°,∠C=(x+36)°,
①∠CAE= (含x的代数式表示)
②求∠F的度数.
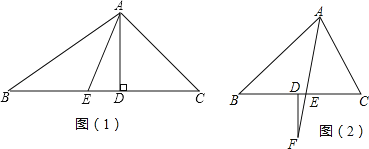
【答案】(1)∠DAE=10°;(2)①72°﹣x°,②∠F=18°.
【解析】试题分析:
(1) 要求∠DAE的度数,可以先求得∠CAE和∠CAD的度数再将它们相减. 先根据三角形的内角和求得∠BAC的度数,再根据AE是∠BAC的角平分线这一条件得到∠CAE的度数. 由于AD是△ABC的高,所以通过直角三角形两锐角的关系可以得到∠CAD的度数. 根据上述角的度数即可求得∠DAE的度数.
(2) 根据三角形的内角和,容易用x表示∠BAC. 根据AF平分∠BAC这一条件,不难用x表示∠CAE和∠BAE. 结合上述结果,利用三角形外角的相关结论,可以得到∠AEC的度数. 根据FD⊥BC,利用对顶角和直角三角形两锐角的关系可以得到∠F的度数.
试题解析:
(1) ∵∠B=30°,∠C=50°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-50°=100°.
∵AE是△ABC的角平分线,即AE平分∠BAC,
∴![]() .
.
∵AD是△ABC的高,即AD⊥BC,
∴在Rt△ADC中,∠CAD=90°-∠C=90°-50°=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2) ①∵∠B=x°,∠C=(x+36)°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-x°-(x+36)°=(144-2x)°.
∵AF平分∠BAC,
∴![]() .
.
故本小题应填写:![]() .
.
②∵AF平分∠BAC,
∴∠BAE=∠CAE=72°-x°.
∵∠AEC是△ABE的一个外角,
∴∠AEC=∠BAE+∠B=72°-x°+x°=72°,
∴∠FED=∠AEC=72°.
∵FD⊥BC,
∴在Rt△EDF中,∠F=90°-∠FED=90°-72°=18°.


科目:初中数学 来源: 题型:
【题目】已知m,n是整数,a≠ 0,b≠ 0,则下列各式中,能表示 “积的乘方法则”的是( )
A. anam=an+m B. (a m)n=a mn C. a0=1 D. (ab)n=anbn
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=50°.
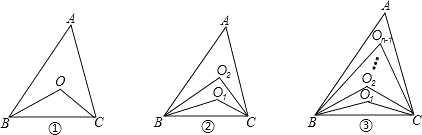
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC= °.
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C= °.
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达终点、用s1、s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是( )
A.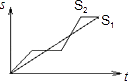
B.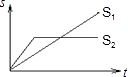
C.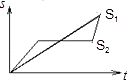
D.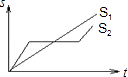
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com