
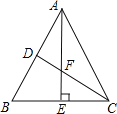
【题目】如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=50°.
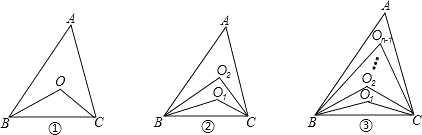
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC= °.
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C= °.
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一组数据中,随机抽取50个作为样本进行统计,在频数分布表中,54.5~57.5这一组的频率是0.12,那么这个样本中的数据落在54.5~57.5之间的有__个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索发现:
如图1,已知直线l1∥l2 , 且l3和l1、l2分别相交于A、B两点,l4和l1、l2分别交于C、D两点,∠ACP记作∠1,∠BDP记作∠2,∠CPD记作∠3.点P在线段AB上.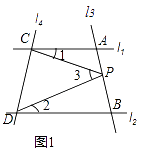
(1)若∠1=20°,∠2=30°,请你求出∠3的度数.
(2)请你根据上述问题,请你找出图1中∠1、∠2、∠3之间的数量关系,并直接写出你的结论.
(3)应用(2)中的结论解答下列问题:如图2,点A在B的北偏东 40°的方向上,在C的北偏西45°的方向上,请你根据上述结论直接写出∠BAC的度数.
拓展延伸:
(4)如果点P在直线l3上且在A、B两点外侧运动时,其他条件不变,试探究∠1、∠2、∠3之间的关系(点P和A、B两点不重合),写出你的结论并说明理由.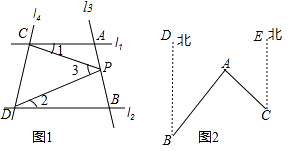
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达终点、用s1、s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是( )
A.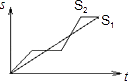
B.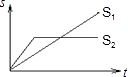
C.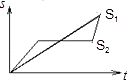
D.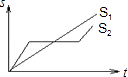
查看答案和解析>>
科目:初中数学 来源: 题型:
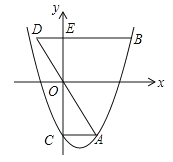
【题目】如图,抛物线![]() (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com