
【题目】如图 , 在菱形ABCD中,∠ABC与∠BAD的度数比为1∶2,周长是32cm . 求:
(1)两条对角线的长度;
(2)菱形的面积.
【答案】
(1)解: 菱形ABCD的周长为32cm,
∴菱形的边长为32÷4=8cm
∵∠ABC∶∠BAD=1∶2,∠ABC+∠BAD=180°(菱形的邻角互补),
∴∠ABC=60°,∠BCD=120°,
∴△ABC是等边三角形,
∴AC=AB=8cm,
∵菱形ABCD对角线AC、BD相交于点O,
∴AO=CO,BO=DO且AC⊥BD,
∴BO=4 ![]() cm,∴BD=8
cm,∴BD=8 ![]() cm
cm
(2)解:菱形的面积: ACBD = ![]() ×8×8
×8×8 ![]() =32
=32 ![]() (cm2)
(cm2)
【解析】(1)根据菱形的性质和菱形ABCD的周长,求出菱形的边长,由菱形的邻角互补,度数比为1∶2,求出∠ABC=60°,得到△ABC是等边三角形;根据菱形的对角线互相垂直平分和勾股定理,求出AC、BD的长;(2)根据菱形的对角线互相垂直平分,求出菱形的面积.


科目:初中数学 来源: 题型:
【题目】如图① ,菱形![]() 中,
中,![]()
![]() ,动点
,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 运动到点
运动到点![]() 停止,动点
停止,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 运动到点
运动到点![]() 停止,它们运动的速度相同.设点
停止,它们运动的速度相同.设点![]() 出发
出发![]() 时,
时,![]() 的面积为
的面积为![]()
![]() .已知
.已知![]() 与
与![]() 之间的函数关系.如图 ②所示,其中
之间的函数关系.如图 ②所示,其中![]() 为线段,曲线
为线段,曲线![]() 为抛物线的一部分,请根据图中的信息,解答下列问题:
为抛物线的一部分,请根据图中的信息,解答下列问题:
(1)当![]() 时,
时,![]() 的面积 (填“变”或“不变”);
的面积 (填“变”或“不变”);
(2)分别求出线段![]() ,曲线
,曲线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是
的面积是![]()
![]() ?
?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A的一次函数图象与正比例函数y=2x的图象相交于点B,则这个一次函数的关系式是( )
A.y=2x+3
B.y= -x+3
C. y=x-3
D.y=2x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了h;
(2)货车的平均速度是km/h;
(3)求线段DE对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,2016年汕头市固定资产投资总额、社会消费品零售总额均突破1500亿元,将1500亿用科学记数法可表示为( )
A.1.5×1011
B.1.5×1012
C.15×1011
D.0.15×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE , DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG , 其中不正确的结论的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
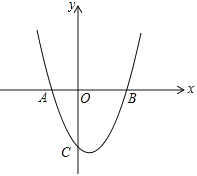
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为![]() .求点H到OM'的距离d的值.
.求点H到OM'的距离d的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com