
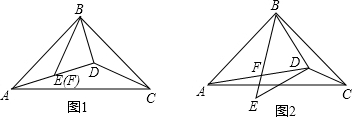
分析 (1)如图1中,作CM⊥BD交BD的延长线于M.由△CBM≌△BAD,推出BD=CM,AD=BM,由AE=DE=BD,推出AD=2BD,BM=2BD,推出BD=DM=CM=$\sqrt{5}$,推出△DCM是等腰直角三角形,由此即可解决问题.
(2)如图2中,作AN⊥BM于N交BE于G,CM⊥BD于M.只要证明△CDM是等腰直角三角形,BN=DN=DM,即可解决问题.
解答 (1)解:如图1中,作CM⊥BD交BD的延长线于M.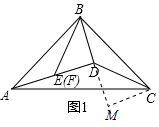
∵∠ADB=∠ABC=90°,
∴∠ABD+∠CBM=90°,∠ABD+∠BAD=90°,
∴∠CBM=∠BAD,
在△CBM和△BAD中,
$\left\{\begin{array}{l}{∠CBM=∠BAD}\\{∠M=∠ADB}\\{BC=BA}\end{array}\right.$,
∴△CBM≌△BAD,
∴BD=CM,AD=BM,
∵AE=DE=BD,
∴AD=2BD,BM=2BD,
∴BD=DM=CM=$\sqrt{5}$,
∴△DCM是等腰直角三角形,
∴CD=$\sqrt{2}$CM=$\sqrt{10}$.
(2)证明:如图2中,作AN⊥BM于N交BE于G,CM⊥BD于M.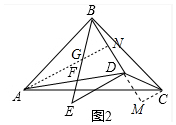
由(1)可知△CBM≌△BAN,
∴BN=CM,AN=BM,
∵AB=AD,AN⊥BD,
∴BN=DN,∵ED⊥BD,
∴AN∥DE,
∴∠GAF=∠FDE,BG=GE,
∴DE=2GN,
在△AGF和△DEF中,
$\left\{\begin{array}{l}{∠GAF=∠FDE}\\{∠AFG=∠DFE}\\{AF=DF}\end{array}\right.$,
∴△AGF≌△DEF,
∴AG=DE=BD,
∴AN=3BN,BM=3CM,
∵BN=DN,
∴DM=CM,
∴△CDM是等腰直角三角形,
∴CD=$\sqrt{2}$CM,
∵CM=BN=$\frac{1}{2}$BD,
∴CD=$\frac{\sqrt{2}}{2}$BD,
∴BD=$\sqrt{2}$CD.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
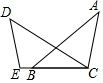 如图,已知B,C,E三点在同一条直线上,∠A=∠DCE,∠ACB=∠E,CD=AB.若BC=8,BE=1,则AC的长为( )
如图,已知B,C,E三点在同一条直线上,∠A=∠DCE,∠ACB=∠E,CD=AB.若BC=8,BE=1,则AC的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
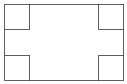 如图所示,在长和宽分别是a、b的矩形纸片的四个角上都剪去一个边长为x的小正方形,折成一个无盖的纸盒.
如图所示,在长和宽分别是a、b的矩形纸片的四个角上都剪去一个边长为x的小正方形,折成一个无盖的纸盒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 62500 | B. | 1000 | C. | 500 | D. | 250 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 “折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.
“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2-(-1)3=2-1=1 | B. | 74-4÷70=70÷70=1 | ||
| C. | $6÷({\frac{1}{3}-\frac{1}{2}})=6×3-6×2=6$ | D. | 23-32=8-9=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
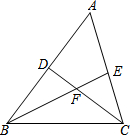 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com