
如图,直线l: 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.

(1)求点A与点B的坐标;
(2)直线m与直线l平行,且与x轴交于点C,与y轴交于点D,若使 ,求直线m的解析式.
,求直线m的解析式.
(1)A(4,0) B(0,3)(2)y=— x+
x+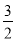 或y=—
或y=—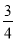 x
x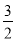
【解析】
试题分析:(1)令x=0,可求点B的坐标;令y=0,可求点A的坐标.
(2)由相似三角形的性质可求出D点坐标,即可确定直线m的解析式.
试题解析:(1)当x=0时,y=3;当y=0时,x=4
∴A(4,0) B(0,3)
(2)∵AB∥CD
∴S△COD∶S△OAB=OD2∶OB2=1∶4
∴OD∶OB=1∶2
∴OD= OB=
OB=
∴D(0,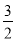 )或(0,-
)或(0,-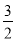 )
)
∴直线m的解析式为y=- x+
x+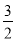 或y=-
或y=-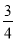 x
x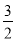
考点:一次函数的应用.
考点分析: 考点1:一次函数 函数的定义:

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源:2014-2015学年山西省大同市矿区七年级上学期期末质量检测数学试卷(解析版) 题型:填空题
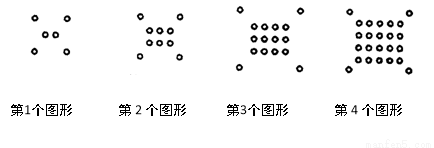
将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形有 个小圆.(用含 n 的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知关于x的方程x2-(k+1)x+ k2+1=0.
k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=4,求该矩形的对角线的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)2间的关系为y=-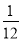 (x-4)2+3,由此可知铅球推出的距离是
(x-4)2+3,由此可知铅球推出的距离是
A.2m B.8m C.10m D.12m
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
方程x2=2x的解是
A.x=2 B.x1=2,x2=0 C.x1=- ,x2=0 D.x=0
,x2=0 D.x=0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:解答题
如图,⊙O是△ABC的外接圆,AB=AC,P是⊙O上一点.

(1)请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线;
(2)结合图②,说明你这样画的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com