
 抛物线y=-x2+2x+n经过点M(-1,0),顶点为C.
抛物线y=-x2+2x+n经过点M(-1,0),顶点为C.分析 (1)直接把M的坐标代入抛物线的解析式即可求出n的值,再利用配方法求顶点C的坐标;
(2)如图1,作辅助线,构建相似三角形,设G(1,a),列方程组求出A、B两点的坐标,根据坐标表示线段的长,证明△APG∽△BQG,列式例式可求出点G的坐标;
(3)设P(m,2m),根据平行四边形的性质得P、Q两点的纵坐标相等,根据P的纵坐标表示出点Q的纵坐标,分三种情况讨论:①当四边形OMQP是平行四边形时,如图2;②当四边形OMPQ是平行四边形,如图3;③当OM是对角线时,如图4,分别表示出点Q的坐标后代入抛物线的解析式可得出点Q的坐标.
解答 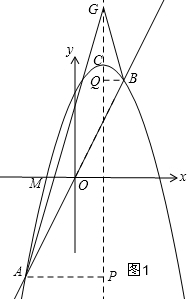 解:(1)把M(-1,0)代入y=-x2+2x+n中得:
解:(1)把M(-1,0)代入y=-x2+2x+n中得:
-1-2+n=0,
n=3,
∴y=-x2+2x+3=-(x2-2x+1-1)+3=-(x-1)2+4,
∴C(1,4);
(2)如图1,存在点G,使∠AGC=∠BGC,
分别过A、B两点作对称轴x=1的垂线AP和BQ,垂足分别为P、Q,
设G(1,a),
则$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=2x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=\sqrt{3}}\\{{y}_{1}=2\sqrt{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\sqrt{3}}\\{{y}_{2}=-2\sqrt{3}}\end{array}\right.$,
∴A(-$\sqrt{3}$,-2$\sqrt{3}$),B($\sqrt{3}$,2$\sqrt{3}$),
∵∠AGC=∠BGC,∠APG=∠BQG=90°,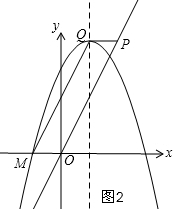
∴△APG∽△BQG,
∴$\frac{AP}{BQ}=\frac{PG}{QG}$,
∴$\frac{\sqrt{3}+1}{\sqrt{3}-1}$=$\frac{a+2\sqrt{3}}{a-2\sqrt{3}}$,
a=6,
∴G(1,6);
(3)设P(m,2m)
①当四边形OMQP是平行四边形时,
如图2,则Q(m-1,2m),
∵点Q在抛物线上,
∴2m=-(m-1)2+2(m-1)+3,
解得:m=0或2,
∴Q1(-1,0)(舍),Q2(1,4),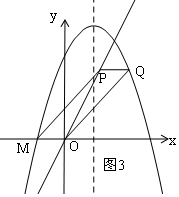
②当四边形OMPQ是平行四边形,
如图3,则Q(m+1,2m),
∵点Q在抛物线上,
∴2m=-(m+1)2+2(m+1)+3,
解得:m=-1$±\sqrt{5}$,
∴Q3(-$\sqrt{5}$,-2-2$\sqrt{5}$),Q4($\sqrt{5}$,-2+2$\sqrt{5}$),
③当OM是对角线时,如图4,
分别过P、Q作x轴的垂线,垂足分别为G、H,
∵四边形MPOQ是平行四边形,
可得△PGM≌△QHO,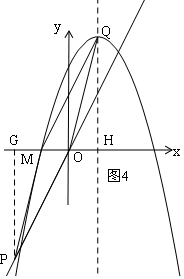
∴GM=OH=-m-1,QH=PG=-2m,
∴Q(-m-1,-2m),
∵点Q在抛物线上,
∴-2m=-(-m-1)2+2(-m-1)+3,
解得:m=0或-2,
∴Q5(-1,0)(舍),Q6(1,4),
综上所述,点Q的坐标是:(1,4)或($\sqrt{5}$,-2-2$\sqrt{5}$)或(-$\sqrt{5}$,-2+2$\sqrt{5}$).
点评 本题是二次函数的综合题,利用待定系数法求二次函数的解析式,由配方法求顶点坐标;本题将函数与几何有机地结合在一起,构建相似三角形,利用坐标表示线段的长,要注意点的象限特点;同时还考查了平行四边形的性质,平行于x轴的直线上的点的纵坐标相等,利用此结论列等式,求出点的坐标.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c的图象如图,其对称轴是直线x=-1,给出下列结论:
已知二次函数y=ax2+bx+c的图象如图,其对称轴是直线x=-1,给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
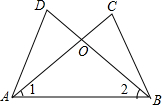 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )| A. | AD=BC | B. | AC=BD | C. | ∠C=∠D | D. | OA=OB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 480 | B. | 360 | C. | 840 | D. | 1080 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com