
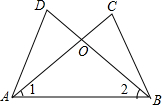
 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )| A. | AD=BC | B. | AC=BD | C. | ∠C=∠D | D. | OA=OB |
分析 A、满足SSA,不能判定△ACB≌△BDA,
B、满足SAS,符合题意,并能判定△ACB≌△BDA,
C、满足AAS,虽然能判定△ACB≌△BDA,但不符合题意,
D、不能判定△ACB≌△BDA.
解答 解:A、添加AD=BC,与已知构成SSA,不能证明△ACB≌△BDA,所以选项A不正确;
B、添加AC=BD,与∠1=∠2和公共边AB=BA构成SAS,能证明△ACB≌△BDA,所以选项B正确;
C、添加∠C=∠D,与∠1=∠2和公共边AB=BA构成AAS,不符合条件,所以选项C不正确;
D、添加OA=OB与∠1=∠2只能是一个条件,与公共边组合,不能证明△ACB≌△BDA,所以选项D不正确.
故选B.
点评 本题考查了全等三角形的判定,在熟练掌握全等三角形的判定方法外,应用全等三角形的判定时,还要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为( )
如图所示,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为( )| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
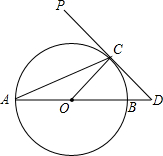 如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )
如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )| A. | 30° | B. | 60° | C. | 67.5° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线y=-x2+2x+n经过点M(-1,0),顶点为C.
抛物线y=-x2+2x+n经过点M(-1,0),顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
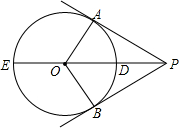 如图所示,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E.
如图所示,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com