

分析 (2)先证明△DEF≌△GCF,得到DE=CG,DF=FG,根据AD=DE,AB=BC,得到BD=BG又因为∠ABC=90°,所以DF=CF且DF⊥BF.
(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,DF=FH,再判断出△DAC≌△HBC,即可得出CD=CH,即可得出结论;
(3)过点B作BH∥ED,与DF的延长线交于点H,连接CH,推出△FDE≌△FHB,求出DF=HF,DE=BH,作AN⊥EB于点N,证△CBH≌△CAD,推出CH=CD,∠DCA=∠BCH,求出∠DCH=90°,即可得出答案.
解答 证明:(1)DF=CF,DF⊥CF
理由:如图1,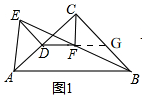
∵∠ADE=∠ACB=90°,
∴DE∥BC,
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE中点,
∴EF=BF.
∴△DEF≌△GBF.
∴DE=GB,DF=GF.
∵AD=DE,
∴AD=GB,
∵AC=BC,
∴AC-AD=BC-GB,
∴DC=GC.
∵∠ACB=90°,
∴△DCG是等腰直角三角形,
∵DF=GF.
∴DF=CF,DF⊥CF.
(2)如图2,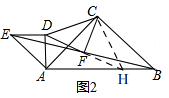
延长DF交BA于点H,
∵△ABC和△ADE是等腰直角三角形,
∴AC=BC,AD=DE.
∴∠AED=∠DAE=∠ABC=45°,
∵CAE=∠BAD=90°,
∵AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF.
∵F是BE的中点,
∴EF=BF,
∴△DEF≌△HBF,
∴DF=HF,ED=HB,
∵AD=ED,
∴AD=HB
在△ADC和△BHC中,$\left\{\begin{array}{l}{AD=HB}\\{∠DAC=∠HBC=45°}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△BHC,
∴DC=HC,
∴△DCH是等腰直角三角形,
∵DF=HF,
∴DF=CF,DF⊥CF;
(3)DF=CF,DF⊥CF;
理由:如图3,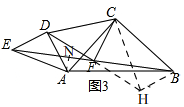
过点B作BH∥ED,与DF的延长线交于点H,连接CH,
∴∠DEF=∠BHF,
在△FDE和△FHB中,$\left\{\begin{array}{l}{∠DEF=∠BHF}\\{EF=BF}\\{∠DFE=∠HFB}\end{array}\right.$,
∴△FDE≌△FHB,
∴DF=FH,DE=HB,
∴AD=ED=HB,
作AN⊥EB于点N,
由已知∠ADE=90°,∠ACB=90°,
可证得∠DEN=∠DAN,∠NAC=∠CBF,
∵BH∥ED,
∴∠DEN=∠HBF,
∴∠CBH=∠CBF+∠HBF=∠NAC+∠DEN=∠NAC+∠DAN=∠CAD,
在△CBH和△CAD中,$\left\{\begin{array}{l}{BC=AC}\\{∠CBH=∠CAD}\\{BH=AD}\end{array}\right.$,
∴△CBH≌△CAD,
∴CH=CD,∠DCA=∠BCH,
∴∠DCH=∠DCA+∠ACH=∠BCH+∠ACH=∠ACB=90°,
∵DF=HF,
∴DF=CF,DF⊥CF.
点评 此题是几何变换综合题,主要考查了旋转的性质,等腰三角形和全等三角形的判定,及勾股定理的运用.要掌握等腰三角形和全等三角形的性质及其判定定理并会灵活应用是解题的关键.


科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c的图象如图,其对称轴是直线x=-1,给出下列结论:
已知二次函数y=ax2+bx+c的图象如图,其对称轴是直线x=-1,给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
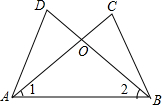 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )| A. | AD=BC | B. | AC=BD | C. | ∠C=∠D | D. | OA=OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com