
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
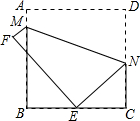 如图,将一张边长为8的正方形纸片ABCD折叠,使点D落在BC的中点E处,点A落在点F处,折痕为MN,则线段MN的长为( )
如图,将一张边长为8的正方形纸片ABCD折叠,使点D落在BC的中点E处,点A落在点F处,折痕为MN,则线段MN的长为( )| A、10 | ||
B、4
| ||
C、
| ||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
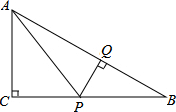 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.
在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.查看答案和解析>>
科目:初中数学 来源: 题型:
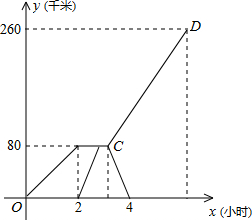 已知,A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
已知,A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
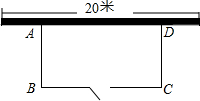 某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地,如图,墙长20米,BC边有一个宽为1米的木门(木门用其它材料做不点用竹篱笆).设养鸡场AB边的长为x米,BC边的长为y米,BC的长度不小于10米且不超过墙长.求y关于x的函数解析式及x的取值范围.
某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地,如图,墙长20米,BC边有一个宽为1米的木门(木门用其它材料做不点用竹篱笆).设养鸡场AB边的长为x米,BC边的长为y米,BC的长度不小于10米且不超过墙长.求y关于x的函数解析式及x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.
如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.查看答案和解析>>
科目:初中数学 来源: 题型:
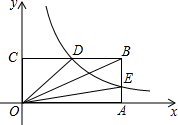 如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数y=
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com