
分析 本题中去甲商场购买所花的费用=餐桌的单价×购买的餐桌的数量+餐椅的单价×实际购买的餐椅的数量(注意要减去赠送的椅子的数量).去乙商场购买所花的费用=(购买的餐桌花的钱+购买餐椅花的钱)×8.5折.如果设餐椅的数量为x,那么可用x表示出到甲、乙两商场购买所需要费用.然后分三种情形列出不等式或方程解决问题,最后写出合适的方案.
解答 解:设学校计划购买x把餐椅,到甲、乙两商场购买所需要费用分别为y甲、y乙,
y甲=200×12+50(x-12),
即:y甲=1800+50x;
y乙=(200×12+50x)×85%,
即y乙=2040+$\frac{85}{2}$x;
①当y甲<y乙时,1800+50x<2040+$\frac{85}{2}$x,
∴x<32,又根据题意可得:x≥12,
∴12≤x<32,
②当y甲=y乙时,1800+50x=2040+$\frac{85}{2}$x,解得x=32,
③当y甲>y乙时,1800+50x=2040+$\frac{85}{2}$x,解得x>32
综上所述,当12<x<32时,到甲商场购买更优惠,
当x=32时,两家商场购买费用相同,
当x>32时,到乙商场购买更优惠.
点评 本题考查不等式的应用,解题关键是要读懂题目的意思,分三种情形列出不等式或方程,这类方案问题是中考常考题型.


科目:初中数学 来源: 题型:解答题
 已知,如图,△ABC是等边三角形,AB=4,点D是AC边上一动点(不与点A、C重合),EF垂直平分BD,分别交AB、BC于点E、F,设CD=x,AE=y.
已知,如图,△ABC是等边三角形,AB=4,点D是AC边上一动点(不与点A、C重合),EF垂直平分BD,分别交AB、BC于点E、F,设CD=x,AE=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
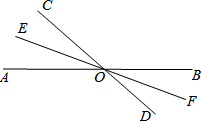 如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?
如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
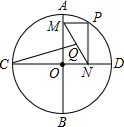 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为$\frac{π}{4}$.
如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为$\frac{π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com