
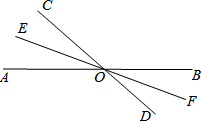
 如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?
如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?分析 根据角平分线的定义、邻补角和对顶角的概念和性质解答.
解答 证明:∵OE、OF分别平分∠AOC、∠BOD,
∴∠EOC=$\frac{1}{2}$∠AOC,
∠FOD=$\frac{1}{2}$∠BOD.(角平分线的定义)
∵直线AB、CD相交于O,
∴∠COD=180°,(平角的定义)
∠AOC=∠BOD,(对顶角相等)
∴∠EOC=∠FOD.
∵∠COD=∠COB+∠BOF+∠FOD=180°.
∴∠COB+∠BOF+∠EOC=180°,(等量代换)
即∠EOF=180°.
∴射线OE、OF在同一条直线上.(共线的判定)
故答案为:AOC;BOD;角平分线的定义;平角的定义;对顶角相等;等量代换,共线的判定.
点评 本题考查的是角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.也考查了邻补角和对顶角.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
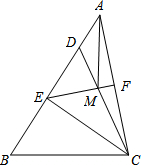 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.
如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,弦CD与AB相交于点E.
如图,AB是⊙O的直径,弦CD与AB相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
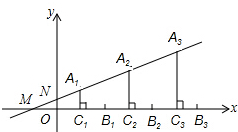 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com