
 如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.
如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$. 分析 首先连接CG,首先证明△CGD≌△CEB,得到△GCE是等腰直角三角形;过点H作AB、BC的垂线,垂足分别为点M、N,进而证明△HEM≌△HCN,得到四边形MBNH为正方形,由此求出CH、HN、CN的长度;最后利用相似三角形Rt△HCN∽Rt△GFH,求出FG的长度.
解答 解:连接CG.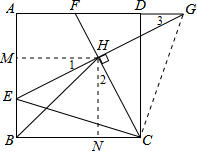 在△CGD与△CEB中,
在△CGD与△CEB中,
$\left\{\begin{array}{l}{BE=DG}\\{∠EBC=∠GDC=90°}\\{BC=DC}\end{array}\right.$,
∴△CGD≌△CEB(SAS),
∴CG=CE,∠GCD=∠ECB,
∴∠GCE=90°,即△GCE是等腰直角三角形.
又∵CH⊥GE,
∴CH=EH=GH.
过点H作AB、BC的垂线,垂足分别为点M、N,则∠MHN=90°,
又∵∠EHC=90°,
∴∠1=∠2,
∴∠HEM=∠HCN.
在△HEM与△HCN中,
$\left\{\begin{array}{l}{∠1=∠2}\\{EH=CH}\\{∠HEM=∠HCN}\end{array}\right.$,
∴△HEM≌△HCN(ASA).
∴HM=HN,
∴四边形MBNH为正方形.
∵BH=8,
∴BN=HN=4$\sqrt{2}$,
∵tan∠FCB=$\frac{HN}{CN}$=2,
∴CN=2$\sqrt{2}$.
在Rt△HCN中,CH=$\sqrt{H{N}^{2}+C{N}^{2}}$=2$\sqrt{10}$.
∴GH=CH=2$\sqrt{10}$.
∵HM∥AG,
∴∠1=∠3,
∴∠2=∠3.
又∵∠HNC=∠GHF=90°,
∴Rt△HCN∽Rt△GFH.
∴$\frac{CH}{FG}=\frac{HN}{GH}$,即$\frac{2\sqrt{10}}{FG}=\frac{4\sqrt{2}}{2\sqrt{10}}$,
∴FG=5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 本题是几何综合题,考查了全等三角形、相似三角形、正方形、等腰直角三角形、勾股定理等重要知识点,难度较大.作出辅助线构造全等三角形与相似三角形,是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).
如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
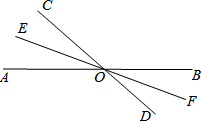 如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?
如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
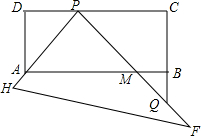 如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.
如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两条弧的长相等,则这两条弧是等弧 | |
| B. | 两条弧的长相等,它们所对的圆心角也相等 | |
| C. | 两个相等的圆心角所对的两条弧的长相等 | |
| D. | 如果两个圆的周长相等,那么它们的半径也相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
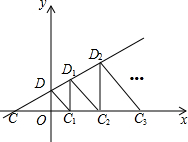 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )| A. | $\frac{4025}{2014}$ | B. | $\frac{{3}^{2012}}{{3}^{2013}}$ | C. | $\frac{{3}^{2013}}{{3}^{2012}}$ | D. | ($\frac{3}{2}$)2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com