
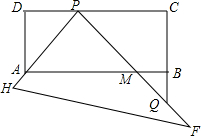
 如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.
如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm. 分析 根据矩形的性质,判定△BAP∽△BMQ,△ADP∽△PCQ,得出比例式,即可求解.
解答 解:设DP=xcm,BQ=ycm.
∵四边形ABCD是矩形,∠HPF=90°,
∴△DAP∽△BMQ,△ADP∽△PCQ,
∴DP:BQ=AD:BM,DP:CQ=AD:PC,
∴DP•BM=AD•BQ,DP•PC=AD•CQ,
∴x=2y,即y=$\frac{x}{2}$,
∴x(5-x)=2(2+$\frac{x}{2}$),
解得:x1=x2=2,
即DP=2cm.
故答案为:2.
点评 本题考查对一元二次方程的应用,而且还得知道矩形的性质,知道相似三角形的性质,可以正确判定相似三角形,解决本题的关键是运用相似三角形的判定定理和性质定理.


科目:初中数学 来源: 题型:填空题
 如图,在Rt△ACB中,∠ACB=90°,点D为BC边上的一点,将线段BD绕点B顺时针方向旋转(点E与点D对应),当BD旋转至与AB垂直时,点A,D,E恰好在同一直线上,作EF⊥BC于点F.若$\frac{CD}{DF}$=$\frac{3}{2}$,AE=5$\sqrt{5}$,则线段AB的长度为10.
如图,在Rt△ACB中,∠ACB=90°,点D为BC边上的一点,将线段BD绕点B顺时针方向旋转(点E与点D对应),当BD旋转至与AB垂直时,点A,D,E恰好在同一直线上,作EF⊥BC于点F.若$\frac{CD}{DF}$=$\frac{3}{2}$,AE=5$\sqrt{5}$,则线段AB的长度为10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.
如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC为等边三角形,点D为BC边上的中点,DF⊥AB于点F,点E在BA的延长线上,且ED=EC,若AE=2,则AF的长为( )
如图,△ABC为等边三角形,点D为BC边上的中点,DF⊥AB于点F,点E在BA的延长线上,且ED=EC,若AE=2,则AF的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$+1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰△ABC中,腰长AB=AC=8厘米,底边BC=6厘米,点D为AB的中点.如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动.当点N的运动速度为2或$\frac{8}{3}$厘米/秒时,能够使△BMD与△CNM全等.
如图,在等腰△ABC中,腰长AB=AC=8厘米,底边BC=6厘米,点D为AB的中点.如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动.当点N的运动速度为2或$\frac{8}{3}$厘米/秒时,能够使△BMD与△CNM全等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com