
分析 (1)根据已知的运算法则和幂的乘方及平方差公式运算即可;
(2)利用(1)中的F(x)=f(x)×g(x),f(x)=2x+2-x,g(x)=2x-2-x 证明即可.
解答 (1)解:∵f(x)=2x+2-x,g(x)=2x-2-x,F(x)=f(x)×g(x),
∴F(2)=f(2)×g(2)=(22+2-2)×(22-2-2)=(22)2-(2-2)2=16-$\frac{1}{16}$=15$\frac{15}{16}$.
故答案为:15$\frac{15}{16}$;
(2)证明:∵f(x)=2x+2-x,g(x)=2x-2-x,
∴F(x)=f(x)×g(x)=(2x+2-x)(2x-2-x)=22x-2-2x,F(-x)=f(-x)×g(-x)=(2-x+2x)(2-x-2x)=2-2x-22x,
∴F(x)+F(-x)=(22x-2-2x)+(2-2x-22x)=0.
点评 本题主要考查了平方差公式,幂的运算法则及新定义运算,根据已知理解新定义运算是解答此题的关键.


科目:初中数学 来源: 题型:解答题
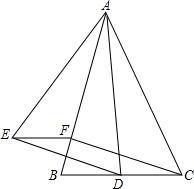 如图,△ABC中,AB=AC,△ABC∽△AED,且D是BC边上任意一点(不与点C重合),作EF∥BC交AB于点F.求证:四边形CDEF是平行四边形.
如图,△ABC中,AB=AC,△ABC∽△AED,且D是BC边上任意一点(不与点C重合),作EF∥BC交AB于点F.求证:四边形CDEF是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/袋) | m | m-2 |
| 售价(元/袋) | 20 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
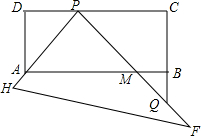 如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.
如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,E、F是对角线AC上的两点,∠DEF=∠EFB.
如图,平行四边形ABCD中,E、F是对角线AC上的两点,∠DEF=∠EFB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com