
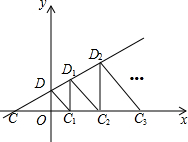
 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )| A. | $\frac{4025}{2014}$ | B. | $\frac{{3}^{2012}}{{3}^{2013}}$ | C. | $\frac{{3}^{2013}}{{3}^{2012}}$ | D. | ($\frac{3}{2}$)2013 |
分析 分别求出C1D1、C2D2、C3D3,发现规律即可解决问题.
解答 解:由图象可知,x=1时,得C1D1=y=$\frac{1}{2}$+1=$\frac{3}{2}$,
x=1+$\frac{3}{2}$=$\frac{5}{2}$时,得C2D2=y=$\frac{1}{2}$×$\frac{5}{2}$+1=$\frac{9}{4}$=($\frac{3}{2}$)2,
x=$\frac{5}{2}$+$\frac{9}{4}$=$\frac{19}{8}$时,得C3D3=y=$\frac{1}{2}$×$\frac{19}{8}$+1=$\frac{27}{8}$=($\frac{3}{2}$)3,
…
C2013D2013=($\frac{3}{2}$)2013,
∴Rt△D2013C2013C2014的腰长是($\frac{3}{2}$)2013.
故选D.
点评 本题考查一次函数的图象与性质、属于规律探究题目,解题的关键是从特殊到一般找到规律,属于中考选择题目的压轴题.


科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.
如图,在正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH.若BH=8,tan∠FCB=2,则FG=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
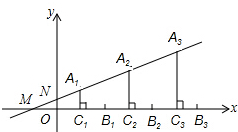 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )| A. | $\frac{3}{5}$ | B. | $\frac{3\sqrt{13}}{13}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{13}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com