
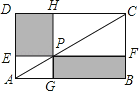
【题目】如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.
【答案】
(1)
证明:
∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC.
∵PF∥AB,
∴PF∥CD,
∴∠CPF=∠PCH.
∵PH∥AD,
∴PH∥BC,
∴∠PCF=∠CPH.
在△PHC和△CFP中,
 ,
,
∴△PHC≌△CFP(ASA).
(2)
证明:∵四边形ABCD为矩形,
∴∠D=∠B=90°.
又∵EF∥AB∥CD,GH∥AD∥BC,
∴四边形PEDH和四边形PFBG都是矩形.
∵EF∥AB,
∴∠CPF=∠CAB.
在Rt△AGP中,∠AGP=90°,
PG=AGtan∠CAB.
在Rt△CFP中,∠CFP=90°,
CF=PFtan∠CPF.
S矩形DEPH=DEEP=CFEP=PFEPtan∠CPF;
S矩形PGBF=PGPF=AGPFtan∠CAB=EPPFtan∠CAB.
∵tan∠CPF=tan∠CAB,
∴S矩形DEPH=S矩形PGBF.
【解析】(1)由矩形的性质得出对边平行,再根据平行线的性质得出相等的角,结合全等三角形的判定定理AAS即可得出△PHC≌△CFP;(2)由矩形的性质找出∠D=∠B=90°,再结合对边互相平行即可证出四边形PEDH和四边形PFBG都是矩形,通过角的正切值,在直角三角形中表示出直角边的关系,利用矩形的面积公式即可得出两矩形面积相等.本题考查了矩形的判定及性质、全等三角形的判定及性质以及平行线的性质,解题的关键是:(1)通过平行找出相等的角;(2)利用矩形的判定定理来证明四边形为矩形.本题属于中档题,难度不大,解决该题型题目时,根据结合矩形的性质及全等三角形的判定定理来解决问题是关键.


科目:初中数学 来源: 题型:
【题目】如图,建筑物AB后有一座假山,其坡度为i=1:![]() ,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )
A.43
B.45
C.51
D.53
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE= ![]() .则四边形ABFE′的面积是 .
.则四边形ABFE′的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣ ![]() x2+
x2+ ![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
(1)判断△ABC的形状,并说明理由;
(2)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一动点,当△PCD的面积最大时,Q从点P出发,先沿适当的路径运动到抛物线的对称轴上点M处,再沿垂直于抛物线对称轴的方向运动到y轴上的点N处,最后沿适当的路径运动到点A处停止.当点Q的运动路径最短时,求点N的坐标及点Q经过的最短路径的长;
(3)如图2,平移抛物线,使抛物线的顶点E在射线AE上移动,点E平移后的对应点为点E′,点A的对应点为点A′,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为点A1 , C1 , 且点A1恰好落在AC上,连接C1A′,C1E′,△A′C1E′是否能为等腰三角形?若能,请求出所有符合条件的点E′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?并求此时对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E为BC上一点,F为DE的中点,且∠BFC=90°.
(1)当E为BC中点时,求证:△BCF≌△DEC;
(2)当BE=2EC时,求 ![]() 的值;
的值;
(3)设CE=1,BE=n,作点C关于DE的对称点C′,连结FC′,AF,若点C′到AF的距离是 ![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
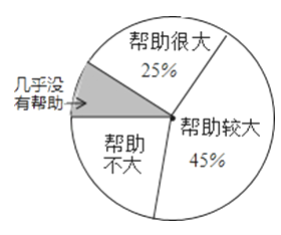
【题目】为了解“数学思想作文对学习帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和如表来表示(图、表都没制作完成).
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 540 | 270 | b |
根据上面图、表提供的信息,解决下列问题:
(1)这次共有多少名学生参与了问卷调查?
(2)求a、b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com