练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，CD是线段AB的垂直平分线，则∠CAD= ∠CBD.请说明理由:

    解:∵CD是线段AB的垂直平分线，

    ∴AC=___ ，_ =BD. .

    在△ACD和△BCD中，

    . =BC，

    AD=_ ，

    CD=CD，

    ∴△ACD≌__ ___ (_ . __) .

    ∴∠CAD=∠CBD (_ __ )

    【答案】BC，AD，AC，BD，△BCD，边边边，全等三角形对应边相等.

    【解析】

    由垂直平分线的性质可得AC=BC，AD=BD，在△ACD和△BCD中，利用“边边边”判定全等，可得∠CAD=∠CBD.

    解：∵CD是线段AB的垂直平分线，

    ∴AC=BC，AD=BD

    在△ACD和△BCD中，

    ∴△ACD≌△BCD（边边边）

    ∴∠CAD=∠CBD（全等三角形对应角相等）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4，则以下四个结论中： ①△BDE是等边三角形； ②AE∥BC； ③△ADE的周长是9； ④∠ADE=∠BDC．其中正确的序号是（　　）

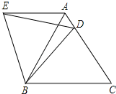
    A.②③④B.①②④C.①②③D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系中的任意两点P1(x1,y1)，P2(x2,y2)，我们把|x1－x2|+|y1－y2|叫做P1、P2两点间的直角距离，记作d(P1,P2)．

    (1) 令P0(2,－3)，O为坐标原点，则d(O,P0)＝ ；

    (2)已知O为坐标原点，动点P(x,y)满足d(O,P)＝1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AB=弧AE，BE分别交AD，AC于点F，G.

    (1)求证：FA＝FG；

    (2)若BD＝DO＝2，求弧EC的长度．

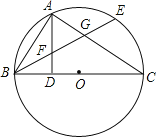
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的试验最有可能的是(　　)

    A. 在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”

    B. 一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃

    C. 暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球

    D. 掷一个质地均匀的正六面体骰子，向上的面点数是4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠C=90°， 点D在AB上，且CD=BD.

    (1)求证:点D是AB的中点.

    (2)以CD为对称轴将△ACD翻折至△A'CD，连接BA'，若∠DBC=a，求∠CB A'的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为5的正方形ABCD中，以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形的个数为（ ）

    A.3B.4C.5D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个二次函数满足以下条件：

    ①函数图象与x轴的交点坐标分别为A（1，0），B（x2，y2）（点B在点A的右侧）；

    ②对称轴是x=3；

    ③该函数有最小值是﹣2．

    （1）请根据以上信息求出二次函数表达式；

    （2）将该函数图象x＞x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”，平行于x轴的直线与图象“G”相交于点C（x3，y3）、D（x4，y4）、E（x5，y5）（x3＜x4＜x5），结合画出的函数图象求x3+x4+x5的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，活动课上，小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度，她先在山脚下的点E处测得山顶A的仰角是30°，然后，她沿着坡度i=1：1的斜坡按速度20米/分步行15分钟到达C处，此时，测得点A的俯角是15°．图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上，求出建筑地所在山坡AE的高度AB．（精确到0.1米，参考数据：≈1.41）．

    查看答案和解析>>

    同步练习册答案