练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】对于平面直角坐标系中的任意两点P1(x1,y1)，P2(x2,y2)，我们把|x1－x2|+|y1－y2|叫做P1、P2两点间的直角距离，记作d(P1,P2)．

    (1) 令P0(2,－3)，O为坐标原点，则d(O,P0)＝ ；

    (2)已知O为坐标原点，动点P(x,y)满足d(O,P)＝1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.

    【答案】(1)5;(2)如图所示.

    【解析】

    （1）、根据直角距离的计算公式进行计算得出答案；

    （2）、根据题意得出|x|+|y|=1，从而得出图形.

    （1）、根据题意得：d（O，P0）=|2﹣0|+|﹣3﹣0|=2+3=5；

    （2）、由题意，得|x|+|y|=1，

    所有符合条件的点P组成的图形如图所示；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在某市实施城中村改造的过程中，“旺鑫”拆迁工程队承包了一项10000 m2的拆迁工程．由于准备工作充分，实际拆迁效率比原计划提高了25%，提前2天完成了任务，请解答下列问题：

    （1）求“旺鑫”拆迁工程队现在平均每天拆迁多少平方米；

    （2）为了尽量减少拆迁给市民带来的不便，在拆迁工作进行了2天后，“旺鑫”拆迁工程队的领导决定加快拆迁工作，将余下的拆迁任务在5天内完成，那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少平方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近日，深圳市人民政府发布了《深圳市可持续发展规划》，提出了要做可持续发展的全球创新城市的目标，某初中学校了解学生的创新意识，组织了全校学生参加创新能力大赛，从中抽取了部分学生成绩，分为5组：A组50～60；B组60～70；C组70～80；D组80～90；E组90～100，统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图．

    （1）抽取学生的总人数是　 　人，扇形C的圆心角是　 　°；

    （2）补全频数直方图；

    （3）该校共有2200名学生，若成绩在70分以下（不含70分）的学生创新意识不强，有待进一步培养，则该校创新意识不强的学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点A，B的坐标分别为（4，0），（3，2）．

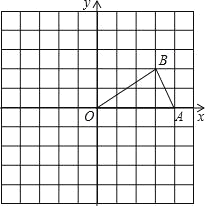
    （1）画出△AOB关于原点O对称的图形△COD；

    （2）将△AOB绕点O按逆时针方向旋转90°得到△EOF，画出△EOF；

    （3）点D的坐标是　 　，点F的坐标是　 　，此图中线段BF和DF的关系是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A，C分别在x轴、y轴的正半轴上，抛物线y＝－x2＋bx＋c经过点B，C两点，点D为抛物线的顶点，连接AC，BD，CD.

    (1)求此抛物线的解析式；

    (2)求此抛物线顶点D的坐标和四边形ABDC的面积．

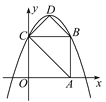
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，本市新建一座圆形人工湖，为测量该湖的半径，小杰和小丽沿湖边选取A，B，C三根木柱，使得A，B之间的距离与A，C之间的距离相等，并测得BC长为120米，A到BC的距离为4米，请你帮他们求出该湖的半径.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，点D在BC上，BD=DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．

    （1）求证：AB是⊙O的直径；

    （2）判断DE与⊙O的位置关系，并加以证明；

    （3）若⊙O的半径为3，∠BAC=60°，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD是线段AB的垂直平分线，则∠CAD= ∠CBD.请说明理由:

    解:∵CD是线段AB的垂直平分线，

    ∴AC=___ ，_ =BD. .

    在△ACD和△BCD中，

    . =BC，

    AD=_ ，

    CD=CD，

    ∴△ACD≌__ ___ (_ . __) .

    ∴∠CAD=∠CBD (_ __ )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“直观三角形”．

    （1）抛物线y=x2的“直观三角形”是　 　．

    A．等腰三角形 B．等边三角形 C．直角三角形 D．等腰直角三角形

    （2）若抛物线y=ax2+2ax﹣3a的“直观三角形”是直角三角形，求a的值；

    （3）如图，面积为12的矩形ABCO的对角线OB在x轴的正半轴上，AC与OB相交于点E，若△ABE是抛物线y=ax2+bx+c的“直观三角形”，求此抛物线的解析式．

    查看答案和解析>>

    同步练习册答案