
【题目】如图,在边长为5的正方形ABCD中,以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形的个数为( )

A.3B.4C.5D.6
【答案】C
【解析】
分别以3为底和以3为腰构造等腰三角形即可.注意等腰三角形的大小不同.
①以A为圆心,以3为半径作弧,交AD、AB两点,连接即可,此时三角形为腰为3的等腰三角形;
②连接AC,在AC上,以A为端点,截取1.5个单位,过这个点作AC的垂线,交AD、AB两点,连接即可
理由如下:∵四边形ABCD为正方形,
∴∠BAC=∠DAC=45°,
∵EF⊥AC
∴△AEH与△AHF为等腰直角三角形
∴EF=EH+FH=AH+AH=3.且AE=AF=![]()
故△AEF为底为3的等腰三角形;
③以A为端点在AB上截取3个单位,以截取的点为圆心,以3个单位为半径画弧,交BC一个点,连接即可,此时三角形为腰为3的等腰三角形;
④连接AC,在AC上,以C为端点,截取1.5个单位,过这个点作AC的垂线,交BC、DC两点,然后连接A与这两个点即可;
理由如下:与②同理可证EF=3,且EC=FC,
在△DEC和△DFC中,
∵AC=AC,∠ACE=∠ACF,EC=FC
∴△DEC≌△DFC
∴AE=AF,
故△AEF为底为3的等腰三角形.
⑤以A为端点在AB上截取3个单位,再作着个线段的垂直平分线交CD一点,连接即可根据垂直平分线上的点到线段两端距离相等,三角形为底为3的等腰三角形.
故满足条件的所有图形如图所示:
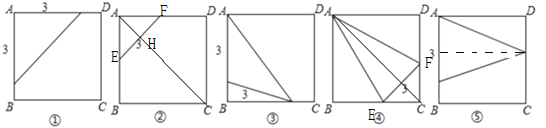
故选C.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是线段AB的垂直平分线,则∠CAD= ∠CBD.请说明理由:

解:∵CD是线段AB的垂直平分线,
∴AC=___ ,_ =BD. .
在△ACD和△BCD中,
. =BC,
AD=_ ,
CD=CD,
∴△ACD≌__ ___ (_ . __) .
∴∠CAD=∠CBD (_ __ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?

![]()

![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 和一次函数y=k2x+b的图象交于点M(3,﹣
和一次函数y=k2x+b的图象交于点M(3,﹣![]() )和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
)和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.

(1)求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积;
(3)拓展提升:如图3,∠E=60°,EC=EB=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“直观三角形”.
(1)抛物线y=x2![]() 的“直观三角形”是 .
的“直观三角形”是 .
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
(2)若抛物线y=ax2+2ax﹣3a的“直观三角形”是直角三角形,求a的值;
(3)如图,面积为12![]() 的矩形ABCO的对角线OB在x轴的正半轴上,AC与OB相交于点E,若△ABE是抛物线y=ax2+bx+c的“直观三角形”,求此抛物线的解析式.
的矩形ABCO的对角线OB在x轴的正半轴上,AC与OB相交于点E,若△ABE是抛物线y=ax2+bx+c的“直观三角形”,求此抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一、二两班共有95人,他们的体育达标率为60%,如果一班的体育达标率为40%,二班达标率为78%,求一、二两班的人数各是多少?若设一、二两班的学生人数各有x人、y人.
(1)填写表:
表格依次填_____,_____,_____,_____,_____.
(2)列出二元一次方程组:_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com