
分析 先利用等比的性质得$\frac{2a+c+e}{2b+d+f}$=$\frac{7}{4}$,而2a+c+e=28,于是可根据内项之积等于外项之积得到2b+d+f的值.
解答 解:∵$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{7}{4}$,
∴$\frac{2a}{2b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{7}{4}$,
∴$\frac{2a+c+e}{2b+d+f}$=$\frac{7}{4}$,
而2a+c+e=28,
∴2b+d+f=$\frac{4}{7}$×28=16.
点评 本题考查了比例的性质:常用的性质有内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
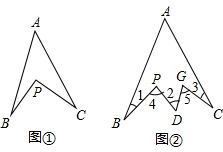 如图1,在∠A内部有一点P,连接BP,CP,请回答下列问题:
如图1,在∠A内部有一点P,连接BP,CP,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
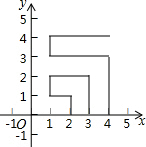 一个粒子从坐标系中的点(1,0)开始沿图方向跳动,第一次跳到(2,0)以后每次跳动一个单位长度,则第2014次跳动后所在位置的坐标为(45,10).
一个粒子从坐标系中的点(1,0)开始沿图方向跳动,第一次跳到(2,0)以后每次跳动一个单位长度,则第2014次跳动后所在位置的坐标为(45,10).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由2x-3=7得2x=7-3 | B. | 由2x-3=x-1得2x-1=x-3 | ||
| C. | 由-3x=5得x=5+3 | D. | 由-$\frac{1}{4}$x=1得x=-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com