
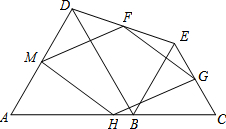
 如图,点A、B、C三点在一条直线上,△ABD、△BCE均为等边三角形,连接DE,点F、G、H、M分别为DE、EC、AC、AD的中点.
如图,点A、B、C三点在一条直线上,△ABD、△BCE均为等边三角形,连接DE,点F、G、H、M分别为DE、EC、AC、AD的中点.分析 连接AE、CD.利用SAS证得△ABE≌△DBC,则AE=CD.然后由三角形中位线定理得到FG=GH=HM=MF,即四边形FGHM是菱形.
解答 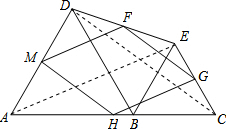 证明:连接AE、CD.
证明:连接AE、CD.
∵△ADB、△BCE为等边三角形
∴AB=DB,BC=BE,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC.
在△ABE和△DBC中,
$\left\{\begin{array}{l}{AB=DB}\\{∠ABE=∠DBC}\\{BC=BE}\end{array}\right.$,
∴△ABE≌△DBC(SAS),
∴AE=CD.
∵点F、G、H、M分别为DE、EC、AC、AD的中点,
∴FG=$\frac{1}{2}$CD,GH=$\frac{1}{2}$AE,HM=$\frac{1}{2}$CD,MF=$\frac{1}{2}$AE,
∴FG=GH=HM=MF,
∴四边形FGHM是菱形.
点评 本题考查了中点四边形,菱形的判定.注意三角形中位线定理在解答中的应用.


科目:初中数学 来源: 题型:解答题
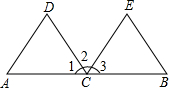 如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
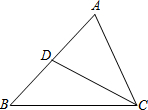 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解瘦西湖风景区中鸟的种类 | |
| B. | 了解扬州电视台《关注》栏目的收视率 | |
| C. | 了解学生对“扬农”牌牛奶的喜爱情况 | |
| D. | 航天飞机发射前的安全检查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com