练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．用反证法证明“三角形的内角中最多有一个角是直角”时应假设：三角形中有两个角是直角．

    分析 在反证法的步骤中，第一步是假设结论不成立，可据此进行填空．

    解答 解：用反证法证明“三角形的内角中最多有一个角是直角”时应假设：三角形中有两个角是直角．
    故答案为：三角形中有两个角是直角．

    点评 此题主要考查了反证法，反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．在假设结论不成立时，要注意考虑结论的反面所有可能的情况，这里三角形中最多有一个是直角的反面是三角形中至少有两个角是直角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．（1）计算：-2-2-$\sqrt{（-\frac{1}{2}）^{2}}$+（π-3.14）0．
    （2）解不等式组$\left\{\begin{array}{l}{2-x＞0}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}\end{array}\right.$，并把解集在数轴上表示出来．
    （3）先化简，再求值：$\frac{{a}^{2}-ab}{{a}^{2}}÷（\frac{a}{b}-\frac{b}{a}$），其中a=$\sqrt{3}$+1，b=$\sqrt{3}$-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC、BD相交于点O，点E在AB上，且BE=BO，求∠EOA的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

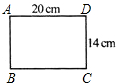    10．如图，木工师傅要以旧翻新一张桌面，打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm，并且与两边相切的圆弧形．请你在木板上把其中一个角的圆弧线画出来（要求尺规作图，保留画图痕迹），并求出新桌面面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

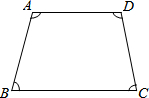    17．多边形的内角和随着边数的变化而变化．设多边形的边数为n，内角和为N，则变量N与n之间的关系可以表示为N=（n-2）•180°．
    例如：如图四边形ABCD的内角和：
    N=∠A+∠B+∠C+∠D=（4-2）×180°=360°
    问：（1）利用这个关系式计算五边形的内角和；
    （2）当一个多边形的内角和N=720°时，求其边数n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知a2+4a+$\sqrt{b+2}$=-4，求|2a+b|-|b-2a|的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．在平面直角坐标系中，已知O是原点，四边形ABCD是长方形，A，B，C的坐标分别为A（-3，1），B（-3，3），C（2，3）．
    （1）求D点坐标；
    （2）将长方形ABCD以每秒1个单位长度的速度水平向右平移，2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少？
    请将（1）（2）中的答案直接填入下表：
     点D A1B1 C1 D1 
     坐标     
    （3）平移（2）中长方形ABCD，几秒钟后△OBD的面积等于长方形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．实验学校计划阻值共青团员372人到某爱国主义基地接受教育，并安排8位老师同行，经学校与汽车出租公司协商，有两种型号客车可供选择，它们的载客量和租金如表所示，为了保证每人都有座位，学校决定租8辆车．
    （1）写出符合要求的租车方案，并说明理由；
    （2）设租甲种客车x辆，总租金共y（元），写出y与x之间的函数关系式；
    （3）在（1）的方案中，求出租金最少的租车方案．
    车种
    人数与租金
    单位     		甲种客车 乙种客车 
     载客量（单位：人/辆） 50 30
     租金（单位：元/辆） 400 200

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如果一只小兔从点A（200，300）先向东跑100米，再向南跑200米到达点B（300，100），那么另一只小兔从点A（200，300）先向北跑100米，再向东跑200米到达点C，则点C的坐标是（400，400）．

    查看答案和解析>>

    同步练习册答案