Question

翻转类的计算问题在全国各地的中考试卷中出现的频率很大，因此初三（5）班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究。你能和小菲一起解决下列各问题吗？（以下各问只要求写出必要的计算过程和简洁的文字说明即可。）

（1）如图①，小菲同学把一个边长为1的正三角形纸片（即△OAB）放在直线l1上，OA边与直线l1重合，然后将三角形纸片向右翻转一周回到初始位置，求顶点O所经过的路程；并求顶点O所经过的路线；

图①

（2）小菲进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l2上，OA边与直线l2重合，然后将正方形纸片向右翻转若干次．她提出了如下问题：

图②

问题①：若正方形纸片OABC接上述方法翻转一周回到初始位置，求顶点O经过的路程；

问题②：正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是。

（3）①小菲又进行了进一步的拓展研究，若把这个正三角形的一边OA与这个正方形的一边OA重合（如图3），然后让这个正三角形在正方形上翻转，直到正三角形第一次回到初始位置（即OAB的相对位置和初始时一样），求顶点O所经过的总路程。

图③

②若把边长为1的正方形OABC放在边长为1的正五边形OABCD上翻转（如图④），直到正方形第一次回到初始位置，求顶点O所经过的总路程。

图④

（4）规律总结，边长相等的两个正多边形，其中一个在另一个上翻转，当翻转后第一次回到初始位置时，该正多边形翻转的次数一定是两正多边形边数的___________。

 

Answer 1

【答案】

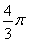(1)；（2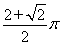），81；（3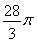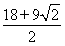），；（4）最小公倍数.

【解析】

试题分析：（1）根据正三角形的性质及弧长公式求出点A绕点B、点C旋转的两段弧长相加即可．

(2)①根据正方形旋转一周的路径，利用弧长计算公式以及扇形面积公式求出即可，

②再利用正方形纸片OABC经过4次旋转得出旋转路径，进而得出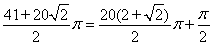 ，即可得出旋转次数．

(3)方法同（2）；

（4）边长相等的两个正多边形，其中一个在另一个上翻转，当翻转后第一次回到初始位置时，该正多边形翻转的次数一定是两正多边形边数的最小公倍数.

试题解析：（1）∵点A所经过的这两段弧所在圆的半径为1，所对圆心角均为120度
∴点A所经过的路线长为.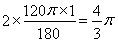

（2）①顶点O经过的总路线长为：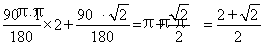

②由①：每翻转一周顶点O经过的总路线长为：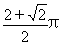

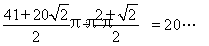
即翻转20周后再翻一次，共翻81次.

（3）①每翻三次翻一周，顶点O所经过的总路线长为：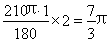

共翻四周回到初始位置，所以顶点O所经过的总路线长为:.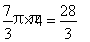

②每翻四次翻一周，顶点O所经过的总路线长为:

共翻5周回到初始位置，所以顶点O所经过的总路线长为：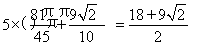

（4）最小公倍数

考点: 1.旋转的性质；2.等边三角形的性质；3.正方形的性质；4.弧长的计算；