练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    阅读下列材料：“思想创新是中国共产党革命、建设与执政经验的历史总结。”“在中国共产党的历史上，思想创新是使我们克服一个又一个困难、战胜一次又一次挑战，从而从各胜利走向另一个胜利的基本保证什么时候思想僵化了，跟不上形势的变化，什么时候就会造成损失，付出代价，陷于被动局面；相反，什么时候能够面对国情，实事求是，什么时候就能使中国革命与建设事业顺利发展。” （11分）
    请回答：
    （1）在20世纪中国共产党革命、建设的创新中产生的两大理论是什么？（2分）
    （2）两大理论解决的主要问题和精髓各是什么？（6分）
    （3）简要分析两大理论产生的共同特点。（3分）
    （1）毛泽东思想和邓小平理论。(2分)
    （2）毛泽东思想主要解决了中国革命走什么道路的问题（1分）
    邓小平理论主要解决的是什么是社会主义和怎么建设社会主义的问题（2分）
    毛泽东思想的精髓是实事求是、群众路线、独立自主（2分）
    邓小平理论的精髓是解放思想、实事求是（1分）
    （3）都是把马克思主义同中国实际相结合进行创新的产物（马克思主义的中国化）；
    都吸取了中国革命和建设的经验和教训；
    都借鉴了外国革命和建设的经验和教训；
    都是中国共产党集体智慧的结晶。（答对其中3点即得3分）解析:
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    仔细阅读下列材料：
    2009×20082008-2008×20092009=
    分析可知，很明显这个题直接计算比较繁，可尝试用x代替2009，y代替2008．
    解：令2009=x，2008=y，则，
    原式=x（y×104+y）-y（x×104+x）=xy×104+xy-xy×104-xy=0
    我们常常“用字母来表示数”，但材料中依据根据问题特点；反而，将较大数字采用恰当的字母来表示，则更能使运算简捷明快．
    （1）仔细阅读材料，在上述问题解决过程中，运用了
     
    思维的方法，体现了
     
    的数学思想．
    （2）给出下面两个问题，参照材料中的方法任选1个小题解答：
    ①计算：
    4018
    20102-2009×2011

    ②若M=
    6789012345
    7890123456
    ，N=
    6789012344
    7890123455
    ，比较M、N的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    24、阅读下列材料，然后回答文后问题．
    如图，在n边形内任取一点O，并把O与各顶点连接起来，共构成n个三角形，这n个三角形的内角和为n•180°，再减去以点O为顶点的一个周角，就可以得到n边形的内角和为（n-2）•180°．
    回答：
    （1）这种方法是将
    多边形
    问题转化为
    三角形
    问题来解决的，这种转化是
    化归
    思想的体现，也正是解决
    多边形
    问题的基本思想；
    （2）若在n边形的一边上或外部任取一点O，并把O与各顶点连接起来，那么如何说明n边形的内角和为（n-2）•180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料，按要求回答问题．
    （1）观察下面两块三角尺，它们有一个共同的性质：∠A=2∠B，我们由此出发来进行思考．
    在图（1）中作斜边上的高CD，由于∠B=30°，可知c=2b，∠ACD=30°，于是AD=
    b
    2
    ，BD=c-
    b
    2
    ，由于△CDB∽△ACB，可知，即a2=c•BD．同理b2=c•AD，于是a2-b2=c（BD-AD）=c（c-b）=bc．对于图（2），由勾股定理有a2=b2+c2，由于b=c，故也有a2-b2=bc．
    在△ABC中，如果一个内角等于另一个内角的2倍，我们称这样的三角形为倍角三角形，两块三角尺都是特殊的倍角三角形，对于任意倍角三角形，上面的结论仍然成立吗？我们暂时把设想作为一种猜测：
    如图（3），在△ABC中，若∠CAB=2∠ABC，则a2-b2=bc．
    在上述由三角尺的性质到“猜测”这一认识过程中，用到了下列四种数学思想方法中的哪一种选出一个正确的并将其序号填在括号内（　　）
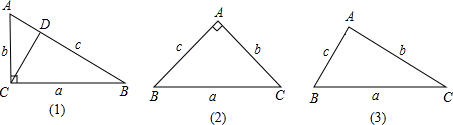    ①分类的思想方法②转化的思想方法③由特殊到一般的思想方法④精英家教网数形结合的思想方法
    （2）这个猜测是否正确，请证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    31、先阅读下列材料，然后完成下列填空：
    点A、B在数轴上分别表示实数 a、b，A、B两点之间的距离表示为|AB|，当A、B两点中有一点在原点时，不妨设A点在原点，如图1|AB|=|OB|=|b|=|b-0|=|a-b|；
    当A、B两点都不在原点时，
    ①如图2，A、B两点都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|
    ②如图3，A、B两点都在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|
    ③如图4，A、B两点分别在原点的两边，|AB|=|OB|+|OA|=|b|+|a|=a+（-b）=|a-b|
    综上所述，
    （1）上述材料用到的数学思想方法是
    数形结合、分类讨论
    （至少写出2个）
    （2）数轴上A、B两点之间的距离|AB|=|a-b|．回答下列问题：
    数轴上表示2和5的两点之间的距离是
    3
    ；数轴上表示-2和-5的两点之间的距离是
    3
    ；数轴上表示1和-4的两点之间的距离是
    5
    ；
    （3）数轴上表示x和-1的两点A和B之间的距离是
    |x+1|
    ；如果|AB|=2，那么x为
    1或-3
    ．

    查看答案和解析>>

    同步练习册答案