
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面五个结论:①AS=AR;②PQ∥AR;③∠SPC+∠BPR=∠PQC;④S四边形ARPQ=$\frac{1}{2}$S△ABC;⑤BR+CS=SQ.其中正确的结论有( )
如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面五个结论:①AS=AR;②PQ∥AR;③∠SPC+∠BPR=∠PQC;④S四边形ARPQ=$\frac{1}{2}$S△ABC;⑤BR+CS=SQ.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2014}{2013}$ | D. | $\frac{1007}{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
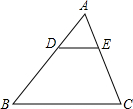 某施工地在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被消去了一个角△ADE,变成了一个梯形BCED,原绿化地一边AB的长由原来的30米缩短成BD长18米,现在的问题是:被消去的部分面积有多大?它的周长是多少?
某施工地在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被消去了一个角△ADE,变成了一个梯形BCED,原绿化地一边AB的长由原来的30米缩短成BD长18米,现在的问题是:被消去的部分面积有多大?它的周长是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com